Synthesis of Constraints for Mathematical Programming with One-Class Genetic Programming

Tomasz P. Pawlak, Krzysztof Krawiec

Abstract

Mathematical Programming models are common in optimization of real-world processes. Models are usually built by optimization experts in an iterative manner: an imperfect model is continuously improved until it approximates the reality well-enough and fulfills all technical requirements (e.g., linearity). In this paper, we propose a Genetic One-Class Constraint Synthesis method (GOCCS) to automatize building of model constraints and lower the burden on the experts. Given a set of exemplary states of normal operation of a business process, GOCCS synthesizes constraints in Linear Programming or Nonlinear Programming form. The synthesized constraints can be accompanied with an arbitrary objective function and supplied to an off-the-shelf solver to find optimal parameters of the process. We assess GOCCS on three families of linear and nonlinear programming benchmarks and conclude promising results. Then, we apply it to a real-world process of wine production, combine the synthesized constraints with an objective function learned from data using least-squares regression and optimize that process.

Access full text

Full text is available at IEEE Xplore.

BibTeX

@ARTICLE{8357939,
author={T. P. {Pawlak} and K. {Krawiec}},
journal={IEEE Transactions on Evolutionary Computation},
title={Synthesis of Constraints for Mathematical Programming With One-Class Genetic Programming},
year={2019},
volume={23},
number={1},
pages={117-129},
keywords={Linear programming;Computational modeling;Programming;Genetic programming;Mathematical model;Benchmark testing;Business process;constraint acquisition;linear programming (LP);model induction;wine quality},
doi={10.1109/TEVC.2018.2835565},
ISSN={1089-778X},
month={Feb},}

Supplementary material

Visualizations of feasible regions

Below, we present visualizations of the feasible regions of the actual models (green) of three synthetic benchmarks: Ball3, Simplex3 and Cube3, and the best-found by GOCCS linear programming models (red).

Ball3: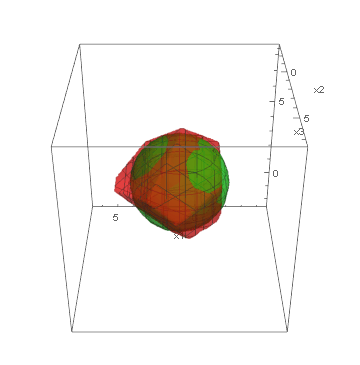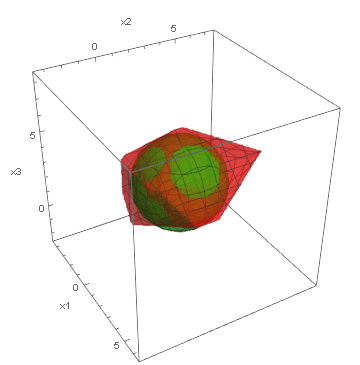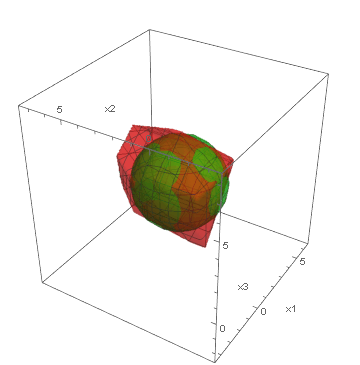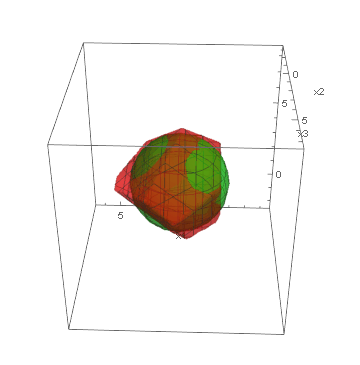
Ball3 benchmark

Simplex3:
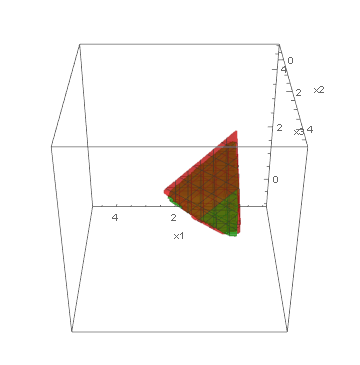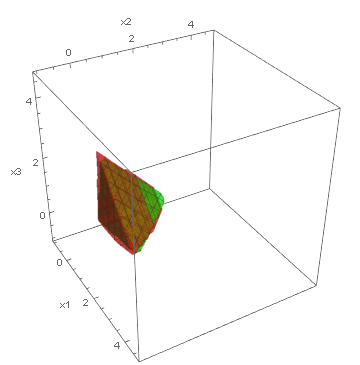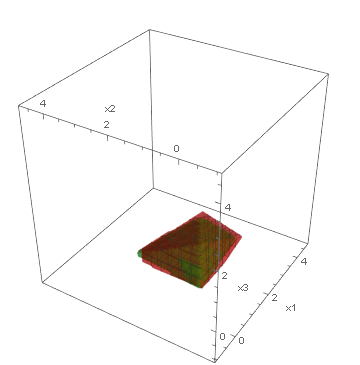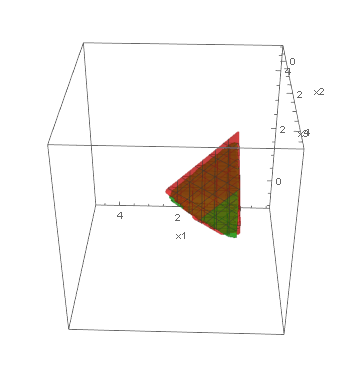
Simplex3 benchmark

Cube3:
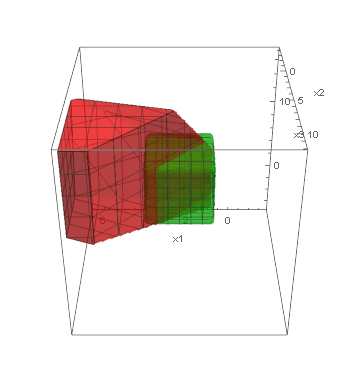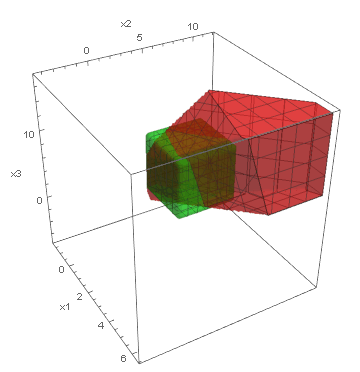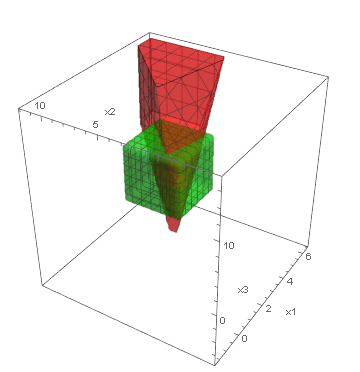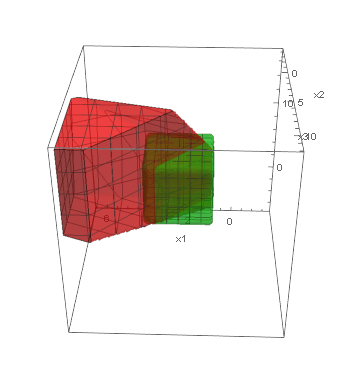
Cube3 benchmark

Source code

The C# source code of the experimental suite presented in the paper is available under conditions of Academic Free License. Visual Studio 2015+ is required to compile binaries from the source. Gurobi Solver 7 is required to run the software. This software runs on Mono 4.4+ under Linux.

Run the software using one of the following commands:

Modeling.MP.exe seed=[random_seed] benchmark=Modeling.Common.Benchmarks.[benchmark] feasibleSamples=[ushort] synthesizer=Modeling.MP.GP.OneClassGPNSGA2Synthesizer CSM=0.1 CSX=0.6 CTM=0.1 CTX=0.1 GCM=0.1 RemoveRedundantConstraints=True linear=True quadratic=[Boolean] MaxGenerations=[uint] PopulationSize=[uint] MinConstraints=[uint] MaxConstraints=[uint] MaxHeight=[uint] output=statistics.sqlite
or:
Modeling.MP.exe seed=[random_seed] problem=[input.csv] synthesizer=Modeling.MP.GP.OneClassGPNSGA2Synthesizer CSM=0.1 CSX=0.6 CTM=0.1 CTX=0.1 GCM=0.1 RemoveRedundantConstraints=True linear=True quadratic=[Boolean] MaxGenerations=[uint] PopulationSize=[uint] MinConstraints=[uint] MaxConstraints=[uint] MaxHeight=[uint] output=statistics.sqlite

« back