Zadania na kolokwium

Temat 1 | Temat 2 | Temat 3 | Temat 4 | Temat 5

Temat 1: Algorytmy sortowania

1. Podaj jaki jest średni i najgorszy czas O(?) działania algorytmu szybkiego sortowania (QS) dla m liczb.

2. Czy ciąg <50,20,8,8,20,10,4,8,8,8,8,1> jest kopcem? Odpowiedź uzasadnij.

3. Jaka jest złożoność obliczeniowa O(?) algorytmu sortowania przez proste wybieranie (Selection sort)?

4. Które spośród podanych algorytmów sortowania sortują w miejscu: szybkie (QS), przez proste wstawianie (IS), pozycyjne (RS), przez zliczanie (CS), stogowe (HS), przez prostą zamianę (BS)?

5. Które algorytmy sortowania najlepiej nadają się do posortowania ciągu liczbowego odwrotnie uporządkowanego i dlaczego?

6. Pokaż kolejne kroki procedury sortującej rosnąco ciąg liczbowy A:12,1,5,4,15,10,8,2,7,5,13,11,3 metodą malejących przyrostów z przyrostami (a) Knutha, (b) Shella.

7. Czy stopień uporządkowania danych wejściowych wpływa na złożoność obliczeniową algorytmu sortowania przez proste wybieranie (SS)?

8. Przedstaw jak będzie wyglądał ciąg liczb <23,1,4,13,90,57,2,18,105> po pierwszej, drugiej i trzeciej iteracji procedury sortującej ten ciąg w porządku malejącym według metody szybkiego sortowania (QS) ze środkowym elementem wyboru. W każdym kroku zaznacz wybrany element i miejsce podziału.

9. Dany jest 10-elementowy wektor liczbowy [2,10,8,11,15,16,31,5,16,6]. Skonstruuj kopiec zawierający wszystkie elementy wektora i przedstaw go w postaci grafu (stogu) oraz w postaci tablicy jednowymiarowej. Podaj definicję struktury kopca.

10. Dla kopca z zadania powyżej pokaż dwa kroki sortowania liczb w porządku rosnącym zgodnie z procedurą sortowania przez kopcowanie (HS). Przedstaw zawartość tablicy oraz stóg po każdym kroku procedury sortowania.

11. Jaki jest czas O(?) działania algorytmu szybkiego sortowania (QS) oraz algorytmu sortowania przez proste wstawianie (IS) dla tablicy wejściowej odwrotnie posortowanej?

12. Dana jest jednowymiarowa tablica liczb [10,11,12,3,17,8,1,5]. Przedstaw zawartość tej tablicy po każdej iteracji procedury sortującej liczby w porządku malejącym metodą bąbelkową (=sortowania przez prostą zamianę / BS).

13. Posortuj ciąg [14,15,4,11,19,3,57,23,15,17,9] metodą sortowania stogowego (HS) do momentu uporządkowania dwóch kolejnych elementów ciągu ilustrując sposób porównywania elementów na stogu. W tym celu należy narysować stóg i zaznaczać, które elementy są zamieniane.

14. Podaj funkcję złożoności obliczeniowej O(?) procedury sortowania n-elementowego ciągu liczbowego w średnim i najgorszym przypadku dla następujących algorytmów sortowania: szybkiego (QS), przez kopcowanie (HS), przez proste wybieranie (SS), przez prostą zamianę (BS) i przez zliczanie (CS).

15. Posortuj ciąg z tablicy [2,3,4,1,3,4,2,5,1,6,7,1] metodą sortowania przez zliczanie (CS) wyjaśniając kolejne etapy sortowania. Podaj i uzasadnij pamięciową i czasową złożoność obliczeniową O(?) tej metody sortowania.

16. Dany jest ciąg liczb naturalnych <45,56,11,47,92,20,8,61,39>. Zbuduj kopiec zawierający wszystkie elementy tego ciągu, stosując standardową metodę przywracania własności kopca (wykorzystywaną w algorytmie Heapsort; najmniejszy element jako korzeń). Przedstaw kopiec w reprezentacji tablicowej. Następnie podziel tablicę zawierającą kopiec po 5-tym elemencie i scal tak powstałe dwa podciągi używając procedury scalania z algorytmu Merge Sort.

17. Czy algorytm sortowania przez zliczanie (CS) jest stabilny? Czym charakteryzuje się własność stabilności algorytmu sortowania?

18. Liczby z tablicy [12,7,9,1,3,5] posortowano w porządku rosnącym wykorzystując standardową procedurę sortowania stogowego (HS). Podczas sortowania kolejność liczb w tablicy zmienia się po każdym elementarnym kroku procedury sortującej. Poniżej podano 6 permutacji liczb z tablicy. Wskaż, które z nich nie wystąpią podczas działania procedury sortujacej:
    [1] 5,7,9,1,3,12    [2] 5,3,1,7,12,9    [3] 1,7,3,5,9,12
    [4] 7,3,5,1,9,12    [5] 5,9,7,1,3,12    [6] 9,7,5,1,3,12

w górę

Temat 2: Złożone struktury danych

1. Utwórz drzewo BST, do którego wczytywane są kolejno wartości kluczy <10,3,15,17,9,12,16>. Jaka będzie kolejność przechodzenia węzłów tego drzewa metodą wzdłużną (preorder)?

2. Zbuduj drzewa poszukiwań binarnych (BST) o wysokości 2 i 4 zawierające zbiór kluczy {2,2,7,17,20,21,32}.

3. Podaj kolejność przechodzenia węzłów drzewa o wysokości 2 z zadania (2) metodą poprzeczną (inorder).

4. Utwórz drzewo poszukiwań binarnych (BST), do którego wczytywane są kolejno wartości kluczy <9,21,7,11,3,5,32>. Który węzeł tego drzewa jest jednocześnie swoim potomkiem i przodkiem właściwym?

5. Zbuduj drzewo poszukiwań binarnych o wysokości 3 zawierające cały zbiór kluczy {110,3,29,108,230,71,20,351}. Czy można zbudować kopiec zawierający wszystkie klucze z tego zbioru?

6. Utwórz drzewo poszukiwań binarnych (BST) o wysokości >2 zawierające wszystkie klucze ze zbioru {10,41,45,50,67,72,99,107,215,218,320}. Następnie usuń z niego dowolny węzeł, który nie jest liściem i pokaż drzewo wynikowe.

7. Podczas przechodzenia poniższych drzew ponumerowano węzły zgodnie z kolejnością ich odwiedzenia. Podaj w jakim porządku (pre-order, in-order, post-order, level-order) przeszukiwano każde drzewo.

   

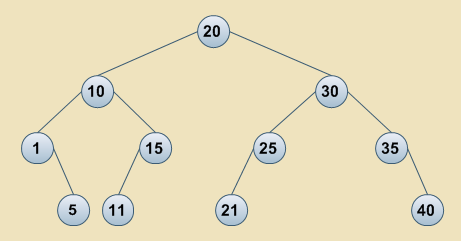
8. Jaka jest złożoność obliczeniowa O(?) procedury wyszukiwania elementu:
   a) w zdegenerowanym drzewie poszukiwań binarnych,
   b) w dokładnie wyważonym drzewie poszukiwań binarnych?

9. Podczas przechodzenia poniższych drzew ponumerowano węzły zgodnie z kolejnością ich odwiedzenia. Podaj w jakim porządku (pre-order, in-order, post-order, level-order) przeszukiwano każde drzewo.

   

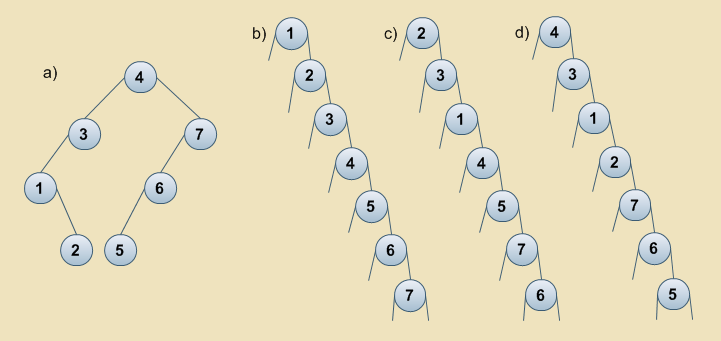
10. Jaka jest wysokość (h=?) drzewa poszukiwań binarnych:
    a) zdegenerowanego,
    b) dokładnie wyważonego
    składającego się z n węzłów? Podaj wysokość w funkcji liczby elementów (węzłów).

11. Utwórz dokładnie wyważone drzewo poszukiwań binarnych wczytując kolejno klucze z ciągu <41,15,50,48,58,5,1,20,38,17,49,100>. Następnie przedstaw proces wstawiania do tego drzewa elementu o kluczu równym "18". Po wstawieniu elementu drzewo powinno zachować własność drzewa dokładnie wyważonego. Pokaż drzewo z wstawionym węzłem.

12. Dane jest drzewo BST o wysokości h=7, zawierające m liczb z przedziału <1,500>. W tym drzewie chcemy wyszukać klucz k=245 zgodnie ze standardową procedurą wyszukiwania elementu w drzewie BST. Które z poniższych ciągów liczbowych mogą zostać sprawdzone podczas poszukiwania klucza k:
    a) 5,401,348,17,309,245
    b) 488,1,377,132,310,147,293,182,245
    c) 100,133,500,184,252,199,117,245
    d) 150,498,211,486,324,221,245?

13. Jaka jest złożoność obliczeniowa O(?) procedury wyszukiwania klucza o minimalej wartości w dokładnie zrównoważonym drzewie poszukiwań binarnych? Podaj odpowiedź w funkcji liczby elementów drzewa.

14. Ile różnych drzew poszukiwań binarnych można utworzyć z 3 liczb o różnych wartościach?

15. Zbuduj drzewo poszukiwań binarnych (BST) dodając do niego kolejno następujące elementy: 10,14,5,7,12,4,6,2,13,16,11,15,9,1,3,8,18,17. Czy tak utworzona struktura jest drzewem wyważonym (AVL)? Uzasadnij odpowiedź.

16. Podaj kolejność przechodzenia węzłów poniższego drzewa w porządkach pre-oder i post-order.

    

17. Jaka jest maksymalna liczba elementów n w dokładnie wyważonym drzewie BST o wysokości h? Odpowiedź sformułuj w postaci funkcji n=f(h).

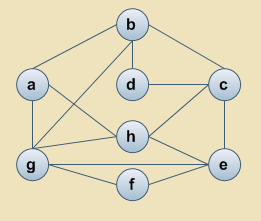
18. Poniższy rysunek przedstawia drzewo BST (a) oraz 3 winorośle (b),(c),(d). Która winorośl powstała z drzewa (a) w wyniku zastosowania rotacji w prawo (algorytm DSW)?

    

w górę

Temat 3: Algorytmy grafowe

1. Wymień 5 różnych reprezentacji maszynowych grafu i podaj ich złożoność pamięciową O(?) stosując następujące oznaczenia: n-liczba wierzchołków, m-liczba krawędzi grafu.

2. Ile pamięci O(?) wymaga zapisanie macierzy incydencji grafu pełnego o k wierzchołkach?

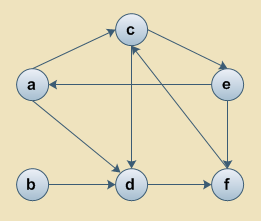
3. Podaj kolejność przechodzenia wierzchołków poniższego grafu metodą przeszukiwania wszerz (BFS). Wierzchołek a jest wierzchołkiem startowym procedury. W procedurze przechodzenia wybieraj następniki w porządku alfabetycznym.

   

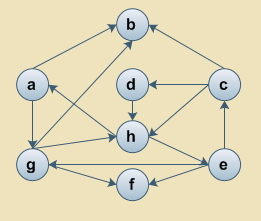
4. Podaj kolejność przechodzenia wierzchołków poniższego grafu metodą przeszukiwania wszerz (BFS). Wierzchołek b potraktuj jako wierzchołek startowy procedury, wybieraj następniki w porządku alfabetycznym.

   

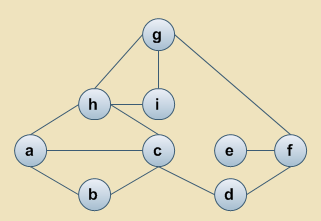
5. Jaka jest złożoność pamięciowa O(?) macierzy sąsiedztwa reprezentującej graf skierowany o k wierzchołkach i m krawędziach?

6. Podaj kolejność przechodzenia wierzchołków poniższego grafu metodą przeszukiwania w głąb (DFS). Wierzchołek b potraktuj jako wierzchołek startowy procedury, wybieraj następniki w porządku alfabetycznym.

   

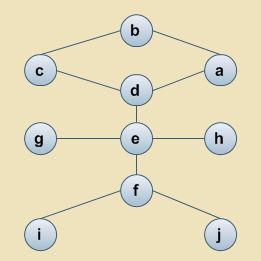
7. Jaka jest złożoność obliczeniowa procedury przeglądania grafu wszerz (BFS) zaimplementowanej z użyciem listy następników, a jaka z użyciem macierzy sąsiedztwa? Podaj odpowiedź w notacji O stosując następujące oznaczenia: n-liczba wierzchołków, m-liczba krawędzi grafu.

8. Podana macierz górnotrójkątna reprezentuje nieskierowany graf z 10-elementowym zbiorem wierzchołków. Wartość "1" oznacza krawędź między wierzchołkami. Wypisz sekwencję wierzchołków otrzymaną w wyniku przeglądania grafu w głąb (DFS) i przedstaw stos obrazujący przebieg obliczeń.

   	1	2	3	4	5	6	7	8	9	10
   1					1	1	1	1
   2			1		1
   3					1				1	1
   4									1	1
   5						1		1
   6
   7									1
   8
   9										1
   10

9. Narysuj dowolny graf skierowany acykliczny o 6-ciu wierzchołkach i 80%-wym nasyceniu grafu krawędziami. Posortuj topologicznie wierzchołki tego grafu. Wykorzystaj algorytm sortowania z przechodzeniem grafu metodą DFS. Podaj czasy odwiedzenia i przetworzenia wierzchołków grafu oraz sekwencję wierzchołków posortowanych w porządku topologicznym.

10. Podaj i uzasadnij złożoność obliczeniową O(?) algorytmu sortowania topologicznego grafu G, wykorzystującego metodę DFS.

11. Posortuj topologicznie wierzchołki poniższego grafu stosując metodę usuwania wierzchołków o zerowym stopniu wejściowym. W procedurze zastosuj porządek alfabetyczny wyboru wierzchołków.

    

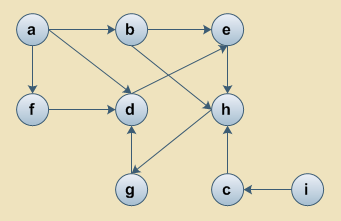
12. Utwórz listę incydencji poprzedników dla poniższego grafu. Czy wierzchołki tego grafu można posortować topologicznie?

    
    

13. Dany jest skierowany graf acykliczny (DAG) reprezentowany w postaci macierzy grafu, listy natępników, listy poprzedników oraz macierzy sąsiedztwa. Dla każdej reprezentacji grafu podaj jaka jest złożoność obliczeniowa O(?) następujących operacji:
    (a) sprawdzenie czy w grafie istnieje łuk (v_i,v_j)
    (b) wyznaczenie zbioru poprzedników wierzchołka v_i
    (c) wyznaczenie zbioru następników wierzchołka v_i
    (d) wyznaczenie zbioru wierzchołków, które nie sąsiadują z v_i.
    Zastosuj następujące oznaczenia: n-liczba wierzchołków grafu G, m-liczba krawędzi grafu G, p_i-liczba poprzedników wierzchołka v_i, s_i-liczba natępników wierzchołka v_i, u_i-liczba wierzchołków, które nie sąsiadują z v_i.

w górę

Temat 4: Algorytmy z powracaniem

1. Jakie są warunki istnienia cyklu Eulera w grafie skierowanym, a jakie w grafie nieskierowanym?

2. Do jakiej klasy złożoności obliczeniowej należy wersja decyzyjna problemu poszukiwania cyklu Hamiltona w grafie?

3. Do jakiej klasy złożoności obliczeniowej należy problem poszukiwania cyklu Eulera w grafie? Czy jest to problem decyzyjny czy optymalizacyjny?

4. Warunkiem koniecznym i wystarczającym istnienia cyklu Eulera w grafie nieskierowanym jest (zaznacz jedno poprawne stwierdzenie):
   (a) nie jest znany odpowiedni warunek
   (b) spójność grafu
   (c) spójność grafu i parzysty stopień każdego wierzchołka
   (d) spójność grafu i parzysty stopień przynajmniej połowy wierzchołków
   (e) w tego typu grafie nie może istnieć cykl Eulera

5. Podaj minimalną liczbę operacji (dodanie/usunięcie wierzchołka/krawędzi) jakie należy wykonać, aby poniższy graf przekształcić w graf Eulerowski.

   

6. Przedstaw krok po kroku działanie algorytmu Fleury'ego na przykładowym grafie nieskierowanym. Jaka jest złożoność obliczeniowa tego algorytmu dla grafu reprezentowanego w postaci macierzy sąsiedztwa?

7. Algorytm z powracaniem dla problemu komiwojażera ma złożoność obliczeniową (zaznacz jedno poprawne stwierdzenie):
   (a) wielomianową
   (b) logarytmiczną
   (c) termin "złożoność obliczeniowa" jest zarezerwowany dla problemów i nie można mówic o złożoności algorytmu
   (d) wykładniczą
   (e) pseudowielomianową

8. Czy istnieje wielomianowy algorytm znajdujący cykl Hamiltona w dowolnym grafie skierowanym? Odpowiedź krótko uzasadnij.

9. Dany jest graf G reprezentowany w postaci listy następników:
   1: 2,4
   2: 6
   3: 1
   4: 7
   5: 1,3
   6: 5,8
   7: 8
   8: 5
   Czy ten graf jest grafem Eulerowskim? Uzasadnij odpowiedź.

10. Czy graf z powyższego zadania jest Hamiltonowski lub pół-Hamiltonowski? Jeśli tak, wypisz odpowiednią sekwencję wierzchołków.

11. Czy prawdziwe są zdania "Cykl Eulera przechodzi przez każdą krawędź grafu nieskierowanego dokładnie jeden raz. Cykl Hamiltona przechodzi przez każdy wierzchołek grafu nieskierowanego dokładnie jeden raz, a tym samym przez każdą krawędź tego grafu co najwyżej jeden raz."?

12. Narysuj:
    a) eulerowski graf skierowany,
    b) pół-eulerowski graf nieskierowany,
    c) hamiltonowski graf nieskierowany,
    d) pół-hamiltonowski graf skierowany o 5-ciu wierzchołkach i dowolnie dobranej liczbie krawędzi.

w górę

Temat 5: Programowanie dynamiczne

1. (5 punktów) Kurier Bonifacy ma do rozwiezienia 6 przesyłek. Dysponuje on plecakiem o ograniczonej pojemności b=8. Każda z przesyłek zajmuje odpowiednio s=[2,1,4,1,4,3] pojemności plecaka. Za dostarczenie przesyłek kurier otrzyma wynagrodzenie odpowiednio w = [7,4,5,1,4,9] Euro. Przesyłki, które nie zmieszczą się do plecaka Bonifacego dostarczy kurier Bonawentura pracujący na drugą zmianę. Korzystając z metody programowania dynamicznego pomóż Bonifacemu podjąć decyzję, które z przesyłek powinien zabrać, aby zmaksymalizować otrzymane wynagrodzenie.

   • Jakie będzie maksymalne wynagrodzenie i które przesyłki zabierze Bonifacy?
   • Podaj wartości z wybranych komórek tablicy kosztów V[i,j] i tablicy decyzyjnej Q[i,j] (gdzie i oznacza przesyłkę, j oznacza pojemność plecaka): V[2,1], V[3,3], V[4,8], V[5,7], V[6,4], Q[3,1], Q[3,5], Q[4,7], Q[6,4], Q[6,6].

2. Podaj algorytm programowania dynamicznego rozwiązujacy problem podziału zbioru. Zastosuj ten algorytm do znalezienia podziału zbioru A=[1,9,5,3,8]. Jaka jest złożoność obliczeniowa tego algorytmu?

3. Napisz ogólny wzór (funkcję rekurencyjną) programowania dynamicznego dla problemu plecakowego.

4. Do jakiej klasy problemów, ze względu na złożoność obliczeniową, należy wersja decyzyjna problemu plecakowego?

5. Zdefiniuj dyskretny problem plecakowy podając i objaśniając funkcję kryterialną oraz parametry problemu. Do jakiej klasy problemów, ze względu na złożoność obliczeniową, należy wersja optymalizacyjna tego problemu?

6. Dana jest instancja problemu plecakowego dla pojemności plecaka b=8:

   element i	rozmiar s(i)	wartość w(i)
   1	2	4
   2	4	5
   3	3	2
   4	1	3
   5	4	3

   Wypełnij tabelę rozwiązań dla tak danego problemu. Zaznacz rozwiązanie optymalne i wypisz, które elementy wchodzą do plecaka oraz podaj ich łączną wartość.

7. Jaka jest złożoność obliczeniowa O(?) algorytmu dokładnego ("brute force") przeszukującego wyczerpująco przestrzeń rozwiązań dla dyskretnego problemu plecakowego?

8. Jaka jest złożoność obliczeniowa O(?) algorytmu programowania dynamicznego dla dyskretnego problemu plecakowego z plecakiem o rozmiarze R oraz liczbie elementów n?

w górę