a) sprawdzający, czy podana liczba jest liczbą automorficzną, tj. znajdującą się na końcu swojego kwadratu, np. 6 jest taką liczbą, ponieważ 62=36.
b) znajdujący wszystkie liczby automorficzne należące do zadanego przedziału liczbowego (użytkownik podaje granice przedziału).
Quicksort: ze zbioru liczb wybieramy jeden (j-ty) element. Pozostałe liczby dzielimy na dwa podzbiory: liczb mniejszych od j-tego elementu (wrzucamy je na lewo) i liczb większych od j-tej (wrzucamy je na prawo). Następnie każdy podzbiór sortujemy zgodnie z procedurą quicksort (rekurencja) itd.
z przedziału (0, 4000) – w systemie rzymskim nie ma jednej ustalonej metody numerowania liczb większych od 3999.
Poniżej podano oznaczenia systemu numeracji.
numeracja arabska: 1 5 10 50 100 500 1000
numeracja rzymska: I V X L C D M
Fragment skali temperaturowej:
C -2 -1 0 1 2 3 4 5
R -1.6 -0.8 0.0 0.8 1.6 2.4 3.2 4.0
F 28.4 30.2 32.0 33.8 35.6 37.4 39.2 41.0
K 271.15 272.15 273.15 274.15 275.15 276.15 277.15 278.15
Oznaczmy przez k pewną liczbę, przez s(k) – sumę wszystkich podzielników liczby k (włącznie z ‘1’ i liczbą ‘k’). Wówczas:
- k jest liczbą niekompletną (deficient number) jeżeli s(k) < 2k
- k jest liczbą doskonałą (perfect number) jeżeli s(k) = 2k
- k jest liczbą zasobną (abundant number) jeżeli s(k) > 2k.
Oznaczmy teraz przez t(k) ilość podzielników liczby k. Jeśli s(k) i t(k) są liczbami doskonałymi, to k jest liczbą wspaniałą (sublime number). Znamy na razie tylko dwie liczby wspaniałe (12 oraz 6 086 555 670 238 378 989 670 371 734 243 169 622 657 830 773 351 885 970 528 324 860 512 791 691 264).
Bubble sort: porównujemy dwie kolejne liczby i jeśli leżą w złej kolejności (np. sortujemy rosnąco, a większy element jest po lewej stronie) zamieniamy je miejscami. Następnie porównujemy kolejne dwie liczby itd. W ten sposób przeglądamy całą listę wiele razy (dopóki nie będzie już można zamienić żadnej pary elementów). Jest to najprostszy i najwolniejszy algorytm sortowania.
Napisz program sprawdzający czy liczba podana przez użytkownika jest liczbą Keitha, gdzie liczbą Keitha nazywamy n-cyfrową liczbę całkowitą K, która tworzy ciąg liczbowy o następujących elementach: pierwsze n wyrazów ciągu jest równych poszczególnym cyfrom liczby K, każdy kolejny wyraz jest sumą poprzedzających go n wyrazów ciągu. Ponadto na którymś miejscu w ciągu pojawia się liczba K.
Przykład: 197 jest liczbą Keitha, gdyż tworzy następujący ciąg (i sama w nim występuje):
| 1, |
9, |
7, |
17, |
33, |
57, |
107, |
197, ... |
| || |
|| |
|| |
|| |
|| |
|| |
||
| cyfry liczby 197 |
1+9+7 |
9+7+17 |
7+17+33 |
17+33+57 |
33+57+107 |
||
Listę liczb Keitha z przedziału <1,1019> znajdziesz tutaj.
Niech A[1..n] będzie tablicą zawierającą n różnych liczb. Jeśli i < j oraz A[i] > A[j], to para (i,j) jest nazywana inwersją A. Na przykład w ciągu: 1,2,5,4,7,12,23,125,41,78,130 inwersjami są pary: (5,4), (125,41) oraz (125,78).
Napisz program poszukujący liczb palindromicznych podzielnych przez k, należących do przedziału <a,b>. Użytkownik podaje wartość k oraz granice przedziału (a i b, przy czym: 0 < a < b < 1 000 000).
Palindromem nazywamy wyraz, który wygląda jednakowo gdy czytamy go od lewej do prawej i od prawej do lewej strony, np. 121 jest liczbą palindromiczną, podobnie 99, 3553, 19791 itp. Nie tylko liczby mogą być palindromami: sformułowanie ‘madam, i’m Adam’ jest nim również.
Napisz program odgadujący kod przyjęty przez użytkownika. Użytkownik koduje cyfry (0-9) zastępując każdą z nich jedną literą alfabetu (a-z). Następnie wykorzystując przyjęty kod wpisuje w programie sumę liczb (podaje od 2 do 6 składników sumy oraz wynik sumowania). Program ma „odgadnąć” jakie znaki przypisano jakim cyfrom (odgaduje tylko te cyfry, które znalazły się w sumie; podaje wszelkie możliwości zakodowania). Użytkownik podając sumę posługuje się wyłącznie literami a-z oraz znakami ‘+’ i ‘-’. Przykład kodowania: 0-a, 1-b, 2-c, 3-d, itd.
Wpisana suma: cfa+bcb+ji=egj (250+121+98=469).
Napisz program zamieniający liczbę zespoloną z postaci z=a+b×i na postać trygonometryczną: z = |z|(cosf + i×sinf). Użytkownik wpisuje liczbę w jednym okienku edycyjnym, liczba ta powinna mieć postać: ±a±bi, przy czym a,b=0,1,2,...
Program ma przedstawić tę samą liczbę w dwóch postaciach trygonometrycznych:
- z wyznaczoną wartością |z| oraz f,
- z wyznaczoną wartością |z|, cosf, sinf.
Przy czym należy wykorzystać wzory: |z|=sqrt(a2+b2), sinf=b/|z|, cosf=a/|z|, f=arctg(b/a).
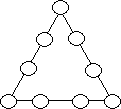
Magiczny trójkąt. Używając liczb z przedziału <1,50> należy rozłożyć je tak, aby sumy cyfr znajdujących się w 4 polach każdego boku trójkąta były takie same. Przy tym każda liczba może być użyta tylko raz. W programie można zaimplementować opcję, która pozwoli użytkownikowi podać wartość sumy, jaką chciałby uzyskać na każdym boku trójkąta. Należy umożliwić podgląd wszystkich znalezionych rozwiązań.
Liczbą pierwszą Mersenne’a nazywamy liczbę pierwszą x, którą można przedstawić w postaci: x=2n-1 (n=1,2,3,...). Początkowe liczby pierwsze Mersenne’a mają następujące wartości: 3, 7, 31, 127, ...
Mówimy, że liczby są przystające modulo k, jeśli ich różnica jest podzielna przez k. Na przykład liczby 3, 10, 17, 24, 31, ... są przystające modulo 7, ponieważ: 10-3=7, 17-10=7, 17-3=14, 31-3=28 itd. Widzimy, że 7, 14, 28 (...) dzielą się bez reszty przez 7 .
Liczbą pierwszą Fermata nazywamy liczbę pierwszą x, którą można przedstawić w postaci: x=2n+1 (n=1,2,3,...). Początkowe liczby pierwsze Fermata: 3, 5, 17, 257, ...
 Rysowanie trójkąta Sierpińskiego (fraktale). Rysujemy na ekranie trójkąt równoramienny T. Kolorujemy go na czarno. Następnie wykonujemy rekurencyjnie następującą procedurę:
Rysowanie trójkąta Sierpińskiego (fraktale). Rysujemy na ekranie trójkąt równoramienny T. Kolorujemy go na czarno. Następnie wykonujemy rekurencyjnie następującą procedurę:1. Znajdujemy środek Si każdego boku trójkąta T; znalezione punkty S1, S2, S3 stają się wierzchołkami nowego trójkąta Tn;
2. Usuwamy trójkąt Tn z trójkąta T (tj. kolorujemy trójkąt Tn na biało);
3. Dla pozostałych 3 części trójkąta T (które są również trójkątami) wykonujemy kroki 1-3 procedury.
Procedurę należy zakończyć po określonej liczbie kroków (liczba ta może być zadana przez użytkownika) lub wtedy, gdy dokonywanie podziałów nie ma już sensu (niczego nie zmienia, gdyż doszliśmy do pojedynczych piksli). Można umożliwić użytkownikowi podgląd wyniku wykonania kolejnej iteracji procedury (np. wstawić do programu przycisk ‘następny krok’, po którego wybraniu dokona się kolejny podział trójkątów).
1. losujemy liczbę z przedziału <1,3> (lub kolor);
2. kolejny punkt gry xi malujemy w punkcie położonym w połowie odcinka pomiędzy poprzednim punktem xi-1 a wierzchołkiem trójkąta o wylosowanym numerze;
3. powtarzamy kroki 1-2 ...
Sekwencja punktów, jakie otrzymujemy w grze nazywa się orbitą (trajektorią) ziarna. Należy sprawdzić, jaki obraz otrzymaliśmy po 100, 500, 1 000, 10 000 iteracjach. Już po 1 000 iteracjach powinniśmy zauważyć, że punkty układają się w trójkąt Sierpińskiego. Figura ta jest zatem atraktorem gry w chaos (tj. chaos prowadzi do deterministycznego kształtu, jakim jest trójkąt Sierpińskiego).
W programie należy umieścić ‘kostkę’ do losowania (np. przycisk) oraz opcję wyboru liczby iteracji gry, która ma się wykonać po wybraniu tej opcji.
Należy napisać program do zmodyfikowanej gry w chaos. Można wybrać jedną z proponowanych modyfikacji (inna figura początkowa, inny współczynnik podziału odcinka):
(a) figura początkowa = trójkąt; jeśli wylosujemy jeden z wierzchołków w podstawy trójkąta, to punkt xi stawiamy jak poprzednio (w połowie odcinka między xi-1 i w), a jeśli wylosujemy wierzchołek górny, to punkt xi stawiamy w odległości 2/3 od xi-1,
(b) figura początkowa = trójkąt; jeśli wylosujemy wierzchołek lewy trójkąta, to punkt xi stawiamy w odległości 1/2 od xi-1, jeśli wylosujemy wierzchołek prawy – punkt stawiamy w odległości 2/3 od xi-1, a jeśli wylosujemy wierzchołek górny, to punkt xi stawiamy w odległości 3/4 od xi-1,
(c) figura początkowa = kwadrat; losujemy spośród 4 liczb; punkt xi stawiamy w odległości 1/2 od punktu poprzedniego xi-1; (niespodzianka – wcale nie otrzymamy dywanu Sierpińskiego; punkty wypełnią cały kwadrat),
(d) figura początkowa = sześciokąt foremny; losujemy spośród 6 liczb; punkt xi stawiamy w odległości 2/3 od punktu xi-1; (otrzymamy sześciokąt Sierpińskiego, którego wewnętrzną granicę stanowi krzywa Kocha przedstawiająca płatek śniegu),
(e) figura początkowa = pięciokąt foremny; losujemy spośród 5 liczb; punkt xi stawiamy w odległości 5/8 od punktu xi-1; (otrzymamy pięciokąt Sierpińskiego);
(a) figura początkowa = trójkąt; jeśli wylosujemy jeden z wierzchołków w podstawy trójkąta, to punkt xi stawiamy jak poprzednio (w połowie odcinka między xi-1 i w), a jeśli wylosujemy wierzchołek górny, to poruszamy się na odległość 1/2 w kierunku wierzchołka, a następnie przeciwnie do ruchu wskazówek zegara obracamy się o 90o wokół wierzchołka i stawiamy punkt xi,
(b) figura początkowa = trójkąt; jeśli wylosujemy jeden z wierzchołków w podstawy trójkąta, to punkt xi stawiamy jak poprzednio (w połowie odcinka między xi-1 i w), a jeśli wylosujemy wierzchołek górny, to poruszamy się na odległość 1/2 w kierunku wierzchołka, a następnie przeciwnie do ruchu wskazówek zegara obracamy się o 180o wokół wierzchołka i stawiamy punkt xi.

Rysowanie dywanu Sierpińskiego (fraktale).
Problem jest podobny do problemu z zadania 40. Figurą wyjściową jest kwadrat, który dzielimy na dziewięć równych części (kwadratów). Usuwamy część leżącą w środku, a każdą pozostałą część dzielimy podobnie jak kwadrat początkowy na 9 części, spośród nich usuwamy część środkową itd.
Należy wykonać maksymalnie 10 podziałów i umożliwić podgląd obrazu po każdej iteracji.
Przykład. Zaszyfrujmy teraz w naszym systemie kryptograficznym słowo „YES”. Najpierw przekształcamy litery słowa na liczby: 24 4 18, potem dodajemy 3 modulo 26: 1 7 21, a na końcu z powrotem przekształcamy na litery: „BHV”.
Przykładowo w równaniu .1.2.3.4.5.6.7.8.9 = 1 istnieje aż 69 sposobów ustawienia ‘+’, ‘-’ lub ‘’ w miejsce kropki, tak że równanie jest spełnione, np. 1+23+4-5+67-89 = 1.
Dalej, należy utworzyć dwie nowe jednowymiarowe tablice dynamiczne T2, T3. Do tablicy T2 program ma przepisać wszystkie liczby parzyste znajdujące się w tablicy T1, natomiast do tablicy T3 – wszystkie liczby nieparzyste z tablicy T1.
Napisz program obliczający ile palindromów wyświetli zegar elektroniczny między godziną g1 i godziną g2. Wszystkie znalezione palindromy z podanego zakresu należy wylistować. Użytkownik podaje w programie godzinę g1 i g2, które tworzą przedział poszukiwań. Godzina może być podana w jednym z następujących formatów: h:mm, hh:mm, h:mm:ss, hh:mm:ss (h – godzina, m – minuta, s – sekunda). Zakładamy, że zegar wyświetla czas w systemie 24-godzinnym, wobec tego: 0 <= h <= 23, 0 <= m <= 59, 0 <= s <= 59 (brak określeń AM, PM). Ponadto g1 <= g2. Użytkownik ma dowolność w określeniu czy znak ":" (dwukropek) należy uwzglęniać przy kwalifikowaniu godziny jako palindromu, czy też można go pominąć.
Przykład. Załóżmy, że pomijamy znak ":", wówczas:
(a) między godziną 0:00 a 23:59 zegar elektroniczny wyświetla 70 palindromów (np. 0:00, 0:50, 3:13, 4:44 itd.)
(b) między godziną 00:00 a 23:59 zegar elektroniczny wyświetla 16 palindromów (np. 00:00, 10:01, 12:21 itd.)
(c) między godziną 0:00:00 a 23:59:59 zegar elektroniczny wyświetla 660 palindromów (np. 0:23:20, 13:22:31 itd.)
(d) między godziną 00:00:00 a 23:59:59 zegar elektroniczny wyświetla 96 palindromów (np. 05:00:50, 14:11:41 itd.)
Definicja palindromów (liczb palindromicznych) znajduje się w zadaniu 27.
Przykładem liczby rozkładalnej na sumę bliźniaków jest liczba 341396 = 55 + 341341.
Liczbą Friedmana nazywamy liczbę całkowitą dodatnią, którą można zapisać w postaci równania, w którym po lewej stronie równania występuje dana liczba, natomiast po prawej stronie – wyrażenie składające się z cyfr danej liczby (i żadnych innych), z których każda musi wystąpić dokładnie raz oraz z operacji: + (dodawanie), - (odejmowanie), × (mnożenie), / (dzielenie), ^ (potęgowanie), () (nawiasy) oraz konkatenacja.
Przykładowe liczby Friedmana:
123456789 = ((86 + 2 × 7)5 - 91) / 34,
987654321 = (8 × (97 + 6 / 2)5 + 1) / 34.
Przykład: 1193 jest kołową liczbą pierwszą, ponieważ:
1193 – jest liczbą pierwszą
1931 – jest liczbą pierwszą
9311 – jest liczbą pierwszą
3119 – jest liczbą pierwszą
Inne liczby pierwsze kołowe: 1, 3, 7, 11, 13, 17, 37, 79, 113, 187, 199, 337, 1193, 3779, 11939, 19937, 193939, 199933, ...
Zauważmy, że liczbą pierwsza kołowa może składać się wyłącznie z cyfr: 1, 3, 7, 9 (wyjątek stanowią liczby jednocyfrowe 2, 5).
(a) na jednej tablicy,
(b) na dwóch tablicach.
Sortowanie przez wstawianie: Sortowanie odbywa się w taki sposób, w jaki sortujemy karty do gry: pobieramy kartę (element) i wstawiamy go plik kart, które już trzymamy; wstawiamy w taki sposób, aby plik kart był posortowany po wstawieniu karty. Podobnie rzecz ma się z dowolnymi elementami, które sortujemy. Załóżmy, że sortujemy elementy w porządku rosnącym. Bierzemy pierwszy element i wstawiamy go w dowolne miejsce pustej tablicy. Następny pobrany element wstawiamy przed poprzednim (jeśli jest mniejszy) lub za poprzednim (jeśli jest większy). Każdy kolejny element wstawiamy tak, żeby wszystkie leżące po jego lewej stronie były od niego mniejsze, a wszystkie leżące po prawej – większe, itd.
- użytkownik może przenosić krążki tylko pojedynczo,
- można wziąć tylko krążek leżący na wierzchu,
- krążek można położyć tylko na pustym paliku lub na krążku większym od trzymanego.
Przykład: pytamy ile liczb pierwszych można stworzyć z cyfr liczby 1379. Potraktujmy liczbę 1379 jako zbiór cyfr {1,3,7,9} i znajdźmy wszystkie podzbiory, które tworzą liczby pierwsze. Okazuje się, że możemy znaleźć aż 31 liczb pierwszych „zanurzonych” w liczbie 1379. Są to: 3, 7, 13, 17, 19, 31, 37, 71, 73, 79, 97, 137, 139, 173, 179, 193, 197, 317, 379, 397, 719, 739, 937, 971, 1973, 3719, 3917, 7193, 9137, 9173, 9371. Uwaga: budując liczbę pierwszą możemy każdą cyfrę ze zbioru wejściowego wziąć tylko raz.