Algorytmy kombinatoryczne w bioinformatyce − Zadanie IV
Przed przystąpieniem do realizacji zadania proszę zapoznać się z wykładem 6.
Mapowanie metodą częściowego trawienia
Problem mapowania metodą częściowego trawienia bazuje na wynikach eksperymentu
z jednym enzymem restrykcyjnym tnącym kopie badanego fragmentu DNA w
odpowiadających mu miejscach restrykcyjnych, lecz w różnych przedziałach
czasowych. Czas trwania trawienia enzymem (w teoretycznym modelu
eksperymentu) dobierany jest w kolejnych reakcjach w taki sposób, aby
enzym przeciął fragment DNA odpowiednio w jednym, w dwóch, itd., w końcu
we wszystkich miejscach restrykcyjnych obecnych w tym fragmencie.
W rezultacie otrzymujemy multizbiór A długości odcinków uzyskanych
we wszystkich takich reakcjach, uzupełniony o długość całego fragmentu.
Należy odtworzyć obraz (mapę) miejsc restrykcyjnych w badanym fragmencie
na podstawie wyników tego eksperymentu, czyli takie rozmieszczenie cięć,
że odległości pomiędzy wszystkimi parami cięć (a także końcami fragmentu DNA)
pokryją się z multizbiorem A.
Przykład: A = {2, 3, 3, 4, 6, 6, 7, 8, 9, 9, 11, 12, 15, 15, 18}.
Mapa = (3, 4, 2, 6, 3).

Zależność liczby cięć k od liczby elementów A można opisać wzorem:
|A| = 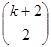 .
.
Problem ten przy założeniu braku błędów w danych wejściowych
jest otwarty z punktu widzenia złożoności obliczeniowej.
Treść zadania:
Należy zaimplementować algorytm dokładny (przeszukiwanie z nawrotami,
o złożoności wykładniczej) realizujący następujące czynności:
− wczytanie z pliku instancji problemu mapowania metodą częściowego
trawienia (multizbioru A);
− skonstruowanie mapy restrykcyjnej zgodnej z podanym multizbiorem
(wystarczy jedna z możliwych map);
− wypisanie rezultatu na wyjściu w sposób czytelny dla użytkownika;
w razie braku rozwiązania (gdyby instancja zawierała błędy) użytkownik
powinien zostać poinformowany odpowiednim komunikatem.
Plik tekstowy zawierający instancję ma składać się z jednego wiersza
z sekwencją liczb naturalnych oddzielonych spacjami.
Aby nie przekazywać programowi informacji o poprawnym uporządkowaniu
odcinków, wartości w pliku powinny wystąpić w innej kolejności niż
w rozwiązaniu.
Każda z osób generuje we własnym zakresie po dwa takie pliki dla każdej
z liczby cięć od 5 do 14 z krokiem 3. Chętni mogą dodatkowo wygenerować
instancje o innej liczbie cięć. Dla każdej instancji należy zapamiętać mapę,
z której została wygenerowana, w celu późniejszej weryfikacji, czy program
działa poprawnie. Instancje nie powinny zawierać błędów.
Program należy przetestować na wygenerowanych instancjach oraz na instancjach
zamieszczonych tutaj.
Warto zbadać wpływ różnych sposobów uporządkowania liczb we wczytywanym ciągu
na czas działania programu. Obliczenia dłuższe niż 1 godz. można przerwać.
Należy także sprawdzić działanie programu dla błędnego wejścia, gdy liczb
jest za mało lub za dużo albo gdy któraś z liczb ma zmienioną wartość.
Celem uniknięcia niepotrzebnych obliczeń program na wstępie powinien
sprawdzać liczebność multizbioru i przechodzić do konstrukcji mapy, tylko jeśli
istnieje liczba cięć przekładająca się na tę liczebność zgodnie z powyższym
symbolem Newtona.
Zarys przykładowej procedury rekurencyjnej można znaleźć
tutaj. Można skorzystać z tego schematu i
zaimplementować na jego podstawie algorytm konstruujący mapę. Procedura
"szukaj" realizuje przeszukiwanie przestrzeni rozwiązań, zagłębiając się
w drzewo kolejnych wywołań procedury, gdzie dojście do liścia na poziomie
"maxind" (równym liczbie elementów mapy) oznacza kompletne rozwiązanie.
Każdy inny węzeł drzewa odpowiada rozwiązaniu częściowemu, które może być
kontynuowane pod warunkiem, że dotychczasowe jego elementy pozostają
w całkowitej zgodności z instancją wejściową. Jeśli nie, należy zaprzestać
dalszego rekurencyjnego zagłębiania się z tego węzła, co spowoduje nawrót
w drzewie wywołań do poziomu wyższego. W przypadku osiągnięcia kompletnego
rozwiązania, co w przykładowej procedurze zapamiętywane jest przez
przypisanie zmiennej "jest" wartości 1, program ma zaprzestać poszukiwania
kolejnych rozwiązań (tutaj dzięki instrukcji "if (*jest==1) break;").
Na slajdzie 22 z wykładu 1 można zobaczyć, jak drzewo wywołań procedury
rekurencyjnej może wyglądać.
Pierwsze wywołanie procedury "szukaj" z wartością 0 w miejscu "ind", czyli
kolejnej pozycji rozwiązania, oznacza poziom zerowy drzewa (jego korzeń)
i puste rozwiązanie. W naszym zadaniu możemy jednak skrócić sobie obliczenia,
gdyż z instancji od razu możemy wywnioskować, który z elementów będzie
pierwszy. Jest nim różnica dwóch największych elementów multizbioru A i jeśli
tylko taki element jest w A (może go nie być na skutek błędu w danych),
wstawiamy go na pierwszą pozycję mapy i uruchamiamy "szukaj" z "ind" równym 1.
Każdy następny element musi już być sprawdzony kolejnymi wywołaniami procedury
"szukaj". Za każdym razem, gdy nowy element miałby zostać dodany do
bieżącego rozwiązania, należy sprawdzić jego zgodność z bieżącym rozwiązaniem,
tzn. czy dla dodanego nowego miejsca restrykcyjnego obecne są w A wszystkie
odległości pomiędzy nim i dotychczas wstawionymi miejscami, a także oboma
końcami cząsteczki. Trzeba przy tym pamiętać, że każdy element A musi być
użyty w rozwiązaniu dokładnie raz, czy to jako element mapy, czy jako suma
innych sąsiadujących elementów. Jeśli w A jakiś element występuje x razy,
dokładnie tyle razy musi być reprezentowany w rozwiązaniu.
Dla przykładowej instancji zamieszczonej powyżej rozpoczynamy z mapą (3,...),
do której dokładać będziemy elementy A spośród jeszcze nieużytych (ani
bezpośrednio, ani jako suma). W tym momencie użytymi elementami A są 3, 15
(jako odległość od pierwszego miejsca restrykcyjnego do "prawego" końca
cząsteczki), 18 (jako odległość pomiędzy końcami cząsteczki). Drugim
elementem mapy mógłby być jeden z
następujących: 2, 3 (druga, niewykorzystana jeszcze trójka), 4, 6 (drugiej
szóstki na tym samym miejscu już się nie sprawdza), 7, itd. Dołożenie 2 dałoby
nam jednak układ (3,2,...), który nie jest akceptowalny, gdyż elementu 5 nie
ma w A. Układ (3,3,...) jest poprawnym częściowym rozwiązaniem, gdyż mamy
w A nieużyte jeszcze elementy 3 (druga trójka), 6 (odległość do "lewego" końca),
12 (odległość do "prawego" końca). Po uaktualnieniu rozwiązania do tej postaci
te trzy wartości muszą zostać oznaczone jako użyte. Proszę, dla pełnego
zrozumienia, rozrysować sobie w analogiczny sposób dalsze kilka węzłów drzewa
wywołań dla tego przykładu. Elementy usuwane z rozwiązania w trakcie nawrotów
(oraz odpowiednie sumy) muszą być z powrotem oznaczane jako nieużyte.
W sprawozdaniu należy zamieścić: opis algorytmu, zawartość wygenerowanych
instancji, wyniki przeprowadzonych testów: uzyskana mapa i czas obliczeń
(czas poniżej 10 sek. należy podać z dokładnością do setnych sekundy), wnioski.
Termin realizacji:
Omówienie zadania: 2 grudnia (grupa wtorkowa)
i 27 listopada (grupy czwartkowe).
Oddanie sprawozdania i zaliczenie zadania: 20 stycznia (grupa wtorkowa)
i 15 stycznia (grupy czwartkowe).
Powrót
Back to the Marta Kasprzak's Home Page
24 Sep 2025


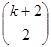 .
.