Another set of experiments were conducted
in two kinds of workstation clusters.
The first one was a cluster of six heterogeneous PC's with
the Linux operating system.
The background load of computers was 'light' but hardly controllable.
The second computer system was dedicated (i.e. 'single user')
pool of six IBM SP-2 processors.
A Parallel Virtual Machine (PVM) was used as
a software environment for experiments.
We present the final results of the experiments only.
A detailed description is given in [DD97].
The star architecture was chosen, and communication models
depicted in Fig.4(a) (equations (6)),
which we will call Model 1,
and Fig.4(b) (equations (7)),
which will be called Model 2,
were assumed.
The application analyzed was distributed file compression
using the LZW method [W84,ZL78].
It is typical of the application that the compression
ratio depends on the size and contents of the compressed file.
The bigger the file the better was the compression obtained.
Hence, in further experiments PEs received
data in chunks of at least 10kB, which was enough to make
the compression ratio relatively stable.
Therefore, it was justified to assume
in equations (6) and (7)
that function ![]() of the amount of returned results
for
of the amount of returned results
for ![]() units of data was
units of data was ![]() .
The coefficient
.
The coefficient ![]() was measured experimentally
(with standard deviation 9%).
Similarly to the previous experiments,
computer processing rates, communication transfer rates
and startup times were measured experimentally.
We believe that communication parameters are relatively stable
because the standard deviation of transmission times was below
was measured experimentally
(with standard deviation 9%).
Similarly to the previous experiments,
computer processing rates, communication transfer rates
and startup times were measured experimentally.
We believe that communication parameters are relatively stable
because the standard deviation of transmission times was below ![]() in SP-2 system, and below
in SP-2 system, and below ![]() in the Linux cluster.
Unfortunately, this was not the case for processing rate parameters.
In the Linux cluster the maximum deviation, depending on the computer,
ranged from
in the Linux cluster.
Unfortunately, this was not the case for processing rate parameters.
In the Linux cluster the maximum deviation, depending on the computer,
ranged from ![]() to
to ![]() .
In the SP-2 computer standard deviation was below
.
In the SP-2 computer standard deviation was below ![]() .
In both computer systems processing rate measurements
became more stable with increasing size of the compressed test file.
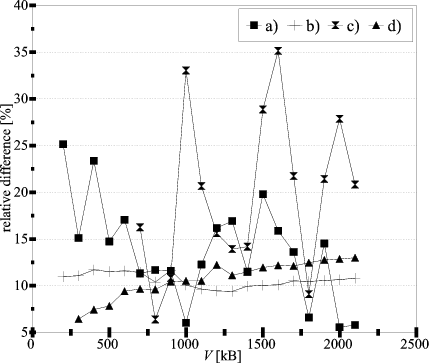
The results of the experiments in both computer clusters
and for the two considered models of returning results
are collected in Fig.9.
.
In both computer systems processing rate measurements
became more stable with increasing size of the compressed test file.
The results of the experiments in both computer clusters
and for the two considered models of returning results
are collected in Fig.9.
 |
We infer that the divisible task concept can be a useful model for distributed applications. Though the model is crude and neglects many details of actual computer systems, a practical verification proved viability of its principles.