Uwagi do wszystkich zestawów:

• Jeśli nie napisano inaczej to obraz wejściowy ma typ numpy.uint8 (czyli liczba całkowita z przedziału [0;255]).

• Jeśli funkcja ma zwracać obraz i nie napisano inaczej to ma on mieć ten sam typ co obraz wejściowy (czyli zazwyczaj numpy.uint8). Dlatego proszę używać funkcji np.rint do zaokrąglenia wartości ułamkowych do najbliższej liczby całkowitej (tam gdzie to jest potrzebne).

Zestaw B* ∞

1. Napisz funkcję zadB1(image, dx, dy) wykonującą przesunięcia obrazu o ułamkowe przesunięcie [dx,dy] (0 <= dx,dy <= 1). W nowym obrazie piksel o współrzędnych (x,y) ma w oryginalnym obrazie współrzędne (x+dx,y+dy), czyli wykonanie tej operacji dokona wizualnego przesunięcie obrazu do góry i w lewo.
   Ponieważ pracujemy na obrazach dyskretnych (w szczególności dyskretnych przestrzennie), do obliczenia wartości pikseli użyj metody interpolacji dwuliniowej. Załóż, że wszystkie piksele leżące poza oryginalnym obrazem mają wartość równą zeru.
   Funkcja ma zwrócić obraz o identycznym rozmiarze jak obraz wejściowy.

   Na poniższym obrazku czarne kropki oznaczają oryginalne położenie pikseli na reprezentowanym obrazie, a niebieskie kropki – położenie piksli na wynikowej bitmapie.

   

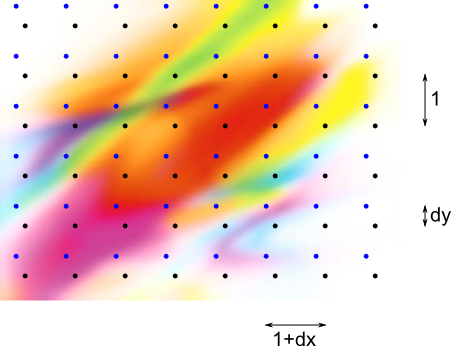
2. Napisz funkcję zadB2(image, width, height) zwracającą nowy obraz (o podanych wymiarach width, height) będący przeskalowaną wersją obrazu image.
   Dla uproszczenia proszę założyć, że:

   1. Obraz wejściowy i wyjściowy mają wymiary przynajmniej 2×2.
   2. Środki narożnikowych pikseli pokrywają się w obrazie oryginalnym i przeskalowanym. W konsekwencji tego piksele narożnikowe w obu obrazach mają zawsze taką samą wartość.

   Do wyliczania wartości pikseli proszę użyć interpolacji dwuliniowej.

   Poniższy obrazek ilustruje oryginalny obrazek o szerokości 8 i wysokości 6 pikseli (czarne kropki) oraz położenie pikseli gdy nowa szerokość to 7 a nowa wysokość to 5.

   

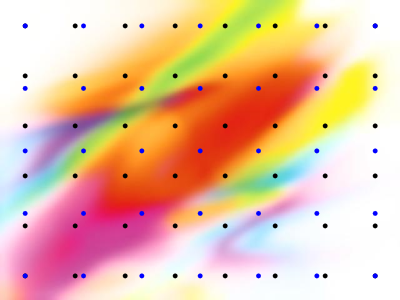
   Do rozwiązanie zadania bez użycia pętli (np. for) może przydać się znajomość indeksowania tablic poprzez inne tablice – patrz opis dla jednego wymiaru oraz opis dla wielu wymiarów.