Fractal Trees
Tree data structures are fundamental to computers. How about using them to generate real trees?
Technologies: #C++ #GLUT #OpenGL
About
How to quickly generate trees? The answer is simple. We can use fractals to generate structures looking just like tree branches. Thanks to Benoit Mandelbrot’s discovery, self-similarity, each part of the branch is a reduced-size copy of the whole.
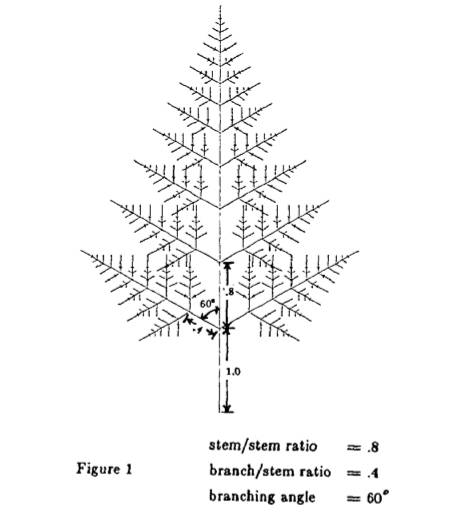
However, to make tree more realistic we use stochastic fractals. Stochastic means that we build it out of probabilities and randomness. In contrast to boring deterministic branching structure we make it statistically self-similar. This guarantees pleasant variety in the tree bark.
This idea came from Peter E. Oppenheimer publication:
Benoit Mandelbrot recognized that the relationship between large scale structure and small scale detail is an important aspect of natural phenomena. He gave the name fractala to objects that exhibit increasing detail as one zooms in closer. If the small scale detail resembles the large scale detail, the object is said to be self-similar.
The geometric notion of fractal self-similarity has become a paradigm for structure in the natural world. Nowhere is this principle more evident than in the world of botany. Recursive branching at many levels of scale, is a primary mechanism of growth in most plants. Analogously, recursive branching algorithms, are furdamental to computers. Many high performance processing engines specialize in tree data structures.
It inspired me to implement my own version of his algorithm using C++ and OpenGL. The effect is satisfying, you can check the source code on my GitHub.
The tree model implemented here has the following features:
- Recursive tree model
- Manual reseeding the random number generator
- Real time design
- Stochastic modelling of tree bark along with topological and geometric parameters
- High resolution renderings
- A detailed parametrization of the geometric relationship between tree nodes
Results

The code has been released on GNU GPL 3.0