Przetwarzanie rozproszone

Niezawodność przetwarzania

dr inż. Arkadiusz Danilecki

W oparciu o wykłady prof. J. Brzezińskiego

Plan wykładu

Podstawowe pojęcia
Kanały komunikacyjne z gwarancjami
Jak formalnie myśleć o poprawności i awariach ?
Detektory awarii
Własności detektorów awarii
Implementacje detektorów awarii
Algorytm detekcji zakończenia statycznego a awarie

Podstawowe pojęcia

Proces poprawny działa zgodnie ze specyfikacją

Wysyła wiadomości wtedy i tylko wtedy, gdy tego oczekujemy, wykonuje kroki algorytmu, ostatecznie osiąga wyznaczone cele...

$$correct(P_i) = \mbox{ true }$$

Podstawowe pojęcia

Proces poprawny działa zgodnie ze specyfikacją

Wysyła wiadomości wtedy i tylko wtedy, gdy tego oczekujemy, wykonuje kroki algorytmu, ostatecznie osiąga wyznaczone cele...

$$correct(P_i) = \mbox{ true }$$

Proces niepoprawny działa niezgodnie ze specyfikacją (w szczególności, nie działa)

... albo prościej - nie jest poprawny

$$\neg correct(P_i) = \mbox{ true }$$

Podstawowe pojęcia: awaria, błąd, wada

ISO/IEC 2382-14:1997(en):

Failure The termination of the ability of a functional unit to perform a required function.

Error A discrepancy between a computed, observed or measured value or condition and the true, specified or theoretically correct value or condition

Fault An abnormal condition that may cause a reduction in, or loss of, the capability of a functional unit to perform a required function.

Podstawowe pojęcia: awaria, błąd, wada

ISO 10303-226

Failure The lack of ability of a component, equipment, sub system, or system to perform its intended function as designed. A failure may be the result of one or many faults

Error ??

Fault an abnormal condition or defect at the component, equipment, or sub-system level which may lead to a failure

Podstawowe pojęcia: awaria, błąd, wada

Federal Standard 1037C

Failure The temporary or permanent termination of the ability of an entity to perform its required function.

Error

The difference between a computed, estimated, or measured value and the true, specified, or theoretically correct value.
A deviation from a correct value caused by a malfunction in a system or a functional unit.

Fault

An accidental condition that causes a functional unit to fail to perform its required function.
A defect that causes a reproducible or catastrophic malfunction.

Podstawowe pojęcia: awaria, błąd, wada

Awaria (ang. failure) - działanie procesu niezgodne z algorytmem czy specyfikacją.

Błąd (ang. error) - część stanu procesu odpowiedzialna za będącą jego następstwem awarię

Wada (ang. fault) - stwierdzona lub hipotetyczna przyczyna wystąpienia błędu

Rodzaje wad

Ukryte (ang. latent) - Wada istnieje, ale jeszcze nie dała żadnych symptomów (manifestujących się jako błędy). Opóźnienie błędu (ang. error latency oznacza czas od pojawienia się wady do manifestacji jej w postaci błędu.

Aktywne (ang. active) - Symptomy wady już się pojawiły i są widoczne.

Rodzaje wad

jednorazowe (ang. transient) - Przy wykonaniu operacji może pojawić się błąd, ale przy ponownym wykonaniu błąd znika.

powtarzalne (ang. intermittent) - W efekcie wady regularnie pojawiają się błędy, zdarzają się też okresy pracy bezbłędnej.

stałe (ang. permanent) - Wada powoduje cały czas błędy przy wykonywaniu operacji aż do wymiany całego komponentu.

Rodzaje wad

Heisenbug - Symptomy wady są różnorakie, błędy często nie pojawiają się przy powtórzeniu operacji mimo replikacji warunków.

Bohrbug - Błędy są powtarzalne przy zreplikowaniu warunków ich występowania, ale ich przyczyna jest nieznana.

Jak sobie radzić z awariami?

Izolowanie (ang. error containment) - Moduły systemu próbują samodzielnie ograniczyć wpływ wad/błędów na działanie innych modułów.

maskowanie (ang. error masking) - Po wykryciu błędu nie powiadamy innych modułów o jego wystąpieniu
fail-fast - Po wykryciu błędu natychmiast powiadamiamy inne moduły lub interfejs użytkownika
fail-stop - Po wykryciu błędu natychmiast zatrzymujemy działanie modułu (czy to jest wtedy awaria?

Jak sobie radzić z awariami?

Replikacja - Zwielokrotnienie komponentów systemu (plus np. algorytmy głosowania). (ang. spatial redundancy).

Restartowanie - Wznawianie pracy komponentów systemu po ich awarii, być może z przywracaniem stanu (ang. time redundancy).

Jak sobie radzić z awariami?

Dywersyfikacja - Komponenty różnią się budową, chociaż dostarczają tę samą funkcjonalność.

Rejuwenacja (rejuvenation) - Restartujemy co jakiś czas, ot tak na wszelki wypadek.

Klasy awarii procesów

Komunikacja... ale z gwarancjami

Kanały niezawodne (perfect): własności

niezawodne dostarczanie (ang. fair loss delivery) - jeżeli wiadomość $M$ wysłana jest przez proces $P_{i}$ do procesu $P_{j}$ i żaden z tych procesów nie ulega awarii (oba są poprawne), to wiadomość $M$ jest dostarczona do $P_{j}$.
brak powielania (ang. no duplication ) - żadna wiadomość $M$ nie jest dostarczona więcej niż raz.
brak samogeneracji (ang. no creation ) - jeżeli wiadomość $M$ została dostarczona do procesu $P_{j}$, to została ona wcześniej wysłana do tego procesu przez jakiś inny proces $P_{i}$. Innymi słowy, kanał nie tworzy samorzutnie wiadomości.

Rozgłaszanie

Nieformalnie, rozgłaszanie to mechanizm komunikacyjny, za pomocą którego proces może wysłać wiadomość do grupy procesów. Mechanizmy rozgłaszania niezawodnego gwarantują pewne własności, pomimo występowania awarii. Gwarancje te tyczą się przede wszystkim zapewnienia dostarczenia wiadomości do adresatów, identyczności zbioru wiadomości dostarczanych do wszystkich procesów poprawnych, oraz kolejności dostarczanych wiadomości.

Rozgłaszanie

Mechanizm a algorytm

MECHANIZM - abstrakcyjna specyfikacja czego chcemy; zbiór własności, które muszą być zagwarantowane procesom korzystającym z mechanizmu.

ALGORYTM - realizuje mechanizm, zapewniając wszystkie gwarancje/własności wyszczególnione w mechanizmie.

Podstawowe rozgłaszanie niezawodne

Własności

WAŻNOŚĆ - jeżeli procesy $\displaystyle P_{i}$ oraz $\displaystyle P_{j}$ są poprawne, to każda wiadomość rozgłaszana przez $\displaystyle P_{i}$ jest ostatecznie dostarczona do $\displaystyle P_{j}$.

BRAK POWIELANIA - jeżeli wiadomość jest dostarczona, to jest dostarczona co najwyżej raz.

BRAK SAMOGENERACJI - jeżeli wiadomość jest dostarczona, to została wcześniej rozgłoszona przez jakiś proces.

Podstawowe rozgłaszanie niezawodne

Algorytm

ZAŁOŻENIE: używamy kanałów niezawodnych (ang. perfect links)


when process ~~P_i~~ wants to broadcast a message ~~m~~ to ~~\mathcal{P}~~ do
    for all ~~P_j \in \mathcal{P}~~ do
        send ~~m~~ to ~~P_j~~
    end for
end when

when a message ~~m~~ arrives at ~~{P}_{i}~~ from ~~{P}_{j}~~ do
	deliver ~~m~~
end when

Podstawowe rozgłaszanie niezawodne

Złożoność

Przy założeniach standardowych (pomijamy czasy przetwarzania lokalnego, przyjmujemy jednostkowy czas przesyłu wiadomości):

czasowa : 1

komunikacyjna : n (zakładając, że wysyłamy sami do siebie również)

Podstawowe rozgłaszanie niezawodne

Poprawność

Zapewnienie wszystkich własności mechanizmu w tym algorytmie wynika wprost z użycia kanałów niezawodnych i ich własności.

Zgodne rozgłaszanie niezawodne

Własności

WAŻNOŚĆ - jeżeli proces $P_{i}$ jest poprawny, to każda wiadomość rozgłaszana przez $P_{i}$ jest ostatecznie dostarczona do $P_{i}$.

BRAK POWIELANIA - jeżeli wiadomość jest dostarczona, to jest dostarczona co najwyżej raz.

BRAK SAMOGENERACJI - jeżeli wiadomość jest dostarczona, to została wcześniej rozgłoszona przez jakiś proces.

ZGODNOŚĆ - jeżeli wiadomość jest dostarczona przez jakiś poprawny proces, to ostatecznie będzie dostarczona przez wszystkie inne poprawne procesy.

Zgodne rozgłaszanie niezawodne

Czy przedstawiony wcześniej algorytm dla mechanizmu podstawowego rozgłaszania niezawodnego zapewnia własności zgodnego rozgłaszania niezawodnego?

Więcej o rozgłaszaniu niezawodnym na Algorytmach Rozproszonych

Modele systemów a rozumowanie o poprawności w obecności awarii

Problemy, które musimy rozważyć:

Jakie cechy systemów są ważne przy analizie poprawności?
Jak opisywać wymagania algorytmów wobec systemu?
Jakie są minimalne wymagania dla danego mechanizmu/algorytmu wobec systemu?

Systemy asynchroniczne

Brak zegara globalnego, brak synchronizacji zegarów
Brak ograniczeń na czas komunikacji
Brak ograniczeń na czas przetwarzania

Systemy synchroniczne

Zegar globalny/synchronizacja zegarów
Znane ograniczenia na czas komunikacji
Znane ograniczenia na czas przetwarzania

Systemy częściowo synchroniczne

Znane są maksymalne czasy komunikacji oraz/lub przetwarzania, lecz nie jest znany moment, po którym zaczną one obowiązywać
Istnieją pewne odcinki czasu, w których system działa jak system asynchroniczny, ale są też okresy, w których system działa jak synchroniczny

Systemy częściowo synchroniczne

synchroniczność procesorów - istnieje stała $k_{0}$ taka, że jeżeli pewien proces $P_{i}$ wykona $k_{0}+1$ kroków, to każdy inny proces wykona co najmniej 1 krok.
istnieją ograniczenia na czas przesyłania wiadomości (opóźnienie komunikacyjne).
porządek wiadomości - porządek synchroniczny oznacza, że jeżeli proces $P_{i}$ wysyła wiadomość $M$ do procesu $P_{j}$ w czasie $\tau _{i}$ oraz proces $P_{k}$ wysyła wiadomość $M'$ do procesu $P_{j}$ w czasie $\tau _{j}>\tau _{i}$, to wiadomość $M$ zostanie dostarczona do $P_{j}$ przed wiadomością $M'$.
rodzaj komunikacji, za pomocą niepodzielnej komunikacji rozgłaszania, czy też za pomocą komunikacji punkt-punkt.
typ operacji send/receive - operacje atomowe (tzn., czy operacja wysłania wiadomości $M$ kończy się dopiero po zakończeniu odbioru tej wiadomości przez adresata), czy też są rozłączne. Innymi słowy, czy komunikacja między procesami jest synchroniczna, czy też nie.

$2^5 = 32$ kombinacje

Detektory awarii

Jeżeli proces działa i kanał jest niezawodny, to w końcu się doczekamy na odpowiedź...

... a więc do rozważań o samej poprawności, wystarczy wiedzieć, które procesy uległy awarii!

Detektory awarii

Rozproszona oraz zawodna "wyrocznia" odpowiadająca na pytania o to, czy dany inny proces działa, czy też nie;

rozproszona - każdy proces może otrzymywać inne odpowiedzi. W praktyce wynika to z tego, że każdy proces będzie miał dostęp de facto do własnej instancji detektora.
zawodna - "wyrocznia" może się mylić, a więc detektor może twierdzić, że poprawny proces jest niepoprawny i na odwrót, detektor może też zmieniać zdanie.

Detektory awarii

${\mathcal {P}}=\{P_{1},P_{2},P_{3},\ldots ,P_{n}\}$
Kanały komunikacyjne są niezawodne.
Zegar globalny jest dyskretny, a jego dziedzina ${\mathcal {T}}$ jest zbiorem liczb naturalnych $\mathbb {N}$.
Czasy komunikacji i przetwarzania są ograniczone lecz nieznane.

Formalna definicja detektora awarii

Niech ${\mathcal {D}}(F)$ oznacza zbiór możliwych historii detektora awarii i jest sumą mnogościową wszystkich możliwych historii detektora awarii, które mogły się przydarzyć z wzorcem awarii $F$ i detektorem awarii $FD$.

$$FD: F(\tau) \rightarrow D(F)$$

Detektor awarii $FD$ jest to funkcja odwzorowująca wzorzec awarii $F$ w zbiór możliwych historii detektora ${\mathcal {D}}(F)$.

Własności detektorów awarii

NIEFORMALNIE

W formalnych definicjach $FD$ odwzorowywał "wzorzec awariii" w zbiór "możliwych historii", tj. rzeczywistemu zachowaniu systemu (gdzie procesy były poprawne lub ulegały awariom) przypisywał "historie detektora" tj. odpowiedzi "ten czy ów proces jest teraz poprawny".

Detektor, który by po prostu losował odpowiedzi, byłby zgodny z tą definicją.

Własności detektorów awarii

NIEFORMALNIE

Jak dobrze możliwe historie naszego detektora odwzorowują faktyczne awarie?

Kompletność (ang. completeness) - zdolność do podejrzewania wszystkich procesów niepoprawnych.

Czy możemy liczyć na to, że nasz (dla przypomnienia - rozproszony!) detektor wykryje awarię?

Dokładność (ang. accuracy) - zdolność do nie podejrzewania wszystkich procesów poprawnych.

Czy możemy ufać naszemu detektorowi, że wykrywa rzeczywiste awarie?

Własności detektorów awarii

Kompletność

Kompletność (ang. completeness) - zdolność do podejrzewania wszystkich procesów niepoprawnych.

Silna Kompletność (ang. strong completeness):

$$\forall F \forall H^{FD} \in D(F), \exists \tau \in \mathcal{T}: \forall P_i \in crashed(F), \forall P_j \in correct(F) : \forall \tau ^i \geq \tau, P_i \in H^{FD}(P_j,\tau ^i ) $$

Dokładność (ang. accuracy) - zdolność do nie podejrzewania wszystkich procesów poprawnych. Czy możemy ufać naszemu detektorowi, że wykrywa rzeczywiste awarie?

Własności detektorów awarii

Kompletność

Kompletność (ang. completeness) - zdolność do podejrzewania wszystkich procesów niepoprawnych.

Silna Kompletność (ang. strong completeness):

$$ \forall P_i: crashed(P_i) \Rightarrow \forall P_j : correct(P_j), \Diamond \Box suspects( P_j, P_i ) $$

$\Diamond$ - eventually, ostatecznie coś się zdarzy;

$\Box$ - always, zawsze coś będzie/jest prawdziwe;

$\Diamond \Box$ ostatecznie dojdzie do tego, że coś będzie już zawsze prawdziwe

Własności detektorów awarii

Dokładność

Dokładność (ang. accuracy) - zdolność do nie podejrzewania wszystkich procesów poprawnych. Czy możemy ufać naszemu detektorowi, że wykrywa rzeczywiste awarie?

Silna dokładność (ang. strong accuracy):

$$ \forall P_i: correct(P_i) \Rightarrow \forall P_j: \Box \neg suspects( P_j, P_i ) $$

Własności detektorów awarii

Dokładność

Dokładność (ang. accuracy) - zdolność do nie podejrzewania wszystkich procesów poprawnych. Czy możemy ufać naszemu detektorowi, że wykrywa rzeczywiste awarie?

Słaba dokładność (ang. weak accuracy):

$$\forall F \forall H^{FD} \in D(F), \forall \tau \in \mathcal{T}, \exists P_i \in correct(F), \forall P_j \not\in F(\tau) : P_i \not\in H^{FD}(P_j,\tau ^i ) $$

Własności detektorów awarii

Dokładność

Dokładność (ang. accuracy) - zdolność do nie podejrzewania wszystkich procesów poprawnych. Czy możemy ufać naszemu detektorowi, że wykrywa rzeczywiste awarie?

Słaba dokładność (ang. weak accuracy):

$$ \exists P_i: correct(P_i) \Rightarrow \forall P_j: \Box \neg suspects( P_j, P_i ) $$

Rodzaje detektorów awarii

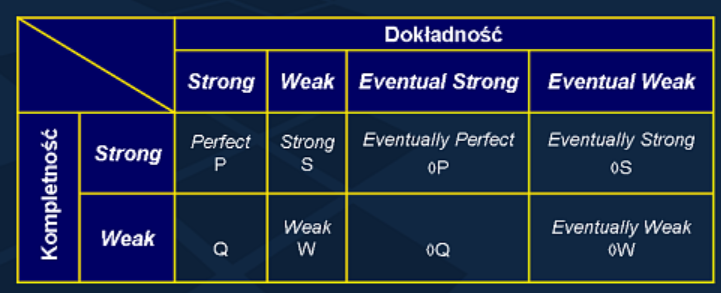
Redukcje i równoważność detektorów awarii

Detektor pewnej klasy może "udawać" detektor innej klasy, w sensie, że wyjście detektora klasy X można z łatwością tak przerobić, by spełniało własności klasy Y.

Gdy relacja ta zachodzi w obie strony, mówimy, że detektory są równoważne

Redukcje i równoważność detektorów awarii

Przykład: detektor klasy P w trywialny sposób może udawać detektor klasy Q (wynika to wprost z definicji - detektor klasy Q różni się tylko słabą kompletnością).

Pokażemy teraz, jak łatwo można zaproponować algorytm symulujący detektor klasy P przy pomocy detektora klasy Q.

Redukcje i równoważność detektorów awarii

Symulowanie klasy $P$ przy pomocy $Q$


				    message $gossip$ is a struct $\left\langle \mbox{set of processId } suspected \right\rangle$

				    local set of processId ~~suspected_i~~ := ~~\emptyset~~ 
				    local const int ~~period_i^{to}~~

Redukcje i równoważność detektorów awarii

Symulowanie klasy $P$ przy pomocy $Q$

~~FD_i~~ jest detektorem klasy ~~Q~~


when a detector ~~FD_i~~ suspects ~~P_j~~ do
    ~~suspected_i \xleftarrow{append} P_j~~
end when

at each ~~period_i^{to}~~ tick at ~~P_i~~ do
    ~~gossip.suspected~~ := ~~suspected_i~~
    send ~~gossip~~ to ~~\mathcal{P}~~
end at each

Redukcje i równoważność detektorów awarii

Symulowanie klasy $P$ przy pomocy $Q$


when message ~~gossip~~ arrives at ~~P_i~~ from ~~P_j~~ do
    ~~suspected_i \xleftarrow{append} gossip.suspected~~
end when

Czy faktycznie spełnimy własności detektora klasy ~~P~~?

Jakość detektorów awarii

Pomyłka: gdy proces poprawny jest błędnie uważany za niepoprawny.

Czas wykrycia awarii
Czas trwania pomyłki
Czas między pomyłkami
Prawdopodobieństwo trafności zapytania
Średni współczynnik pomyłek
Okres pracy bezbłędnej

Czas wykrycia awarii

Czas trwania pomyłki

Czas między pomyłkami

Detektory "przyrostowe"

Tradycyjne detektory: wartość podejrzewam lub nie podejrzewam.

Detektory przyrostowe (ang. accrual failure detector): wartością jest liczba rzeczywista określająca prawdopodobieństwo, czy proces uległ awarii.

Przykładowa implementacja: obserwacja zachowania pulsu w przeszłości i wyliczanie na tej podstawie prawdopodobieństwa, czy pewnym okresie puls przychodzi z opóźnieniem, czy też proces uległ awarii.

Które jest bardziej zrozumiałe?


    ~~suspected_i~~ := ~~suspected_i \cup gossip.suspected~~
    ~~suspected_i \leftarrow gossip.suspected~~
    ~~suspected_i \xleftarrow{append} gossip.suspected~~
    ~~var_i, var_j~~ := ~~val^1, val^2~~
    ~~var_i\langle field^1, field^2\rangle~~ := ~~\langle val^1, val^2 \rangle~~
   send ~~\langle field^1 = val^1, field^2 = val^2\rangle~~ to ~~P_j~~