Przetwarzanie rozproszone
Czas wirtualny + złożoność i poprawność dr inż. Arkadiusz Danilecki
Plan wykładu
- Czas wirtualny
- Zegary skalarne Lamporta
- Zegary wektorowe Matterna
- Warunki poprawności algorytmów
- Złożoność komunikacyjna i czasowa
Czas w systemie rozproszonym
Zegar każdego węzła w systemie jest niezależny.

Czy można by po prostu zsynchronizować zegary?

Rozwiązanie: czas wirtualny, odzwierciedlający tylko logicznie zachodzące w systemie zdarzenia i stanowiący tylko aproksymację czasu rzeczywistego.
Rozwiązanie
Każdemu zdarzeniu przypisujemy etykietę zegarową
Ustalamy relację porządku między etykietami zegarowymi
Formalnie...
Zegarem logicznym systemu rozproszonego nazywamy pewien abstrakcyjny mechanizm, który każdemu zdarzeniu $E\in {\mathcal E}$, przyporządkuje wartość $\mathcal{T}( E )$ z przeciwdziedziny ${\mathcal {Y}}$, tak by zachować logiczne zależności między zdarzeniami.
Jeszcze bardziej formalnie..
$$ \forall E, E^{\prime} \in \mathcal{E} :: E \mapsto E^{\prime} \implies \mathcal{T}(E) < \mathcal{T}(E^{\prime})$$
Minimalne własności
Jeżeli lokalne zdarzenie $E_i^k$ w procesie $P_i$ poprzedza lokalnie inne zdarzenie lokalne $E_i^l$, to znacznik czasowy dla $E_i^k$ musi być mniejszy niż $E_i^l$
Wysłanie wiadomości musi być postrzegane jako wcześniejsze niż odebranie tej samej wiadomości, tzn wartości zegara dla wysłania wiadomości muszą być mniejsze niż dla odebrania tejże wiadomości.
Zegary skalarne
Zegarem logicznym systemu rozproszonego nazywamy pewien abstrakcyjny mechanizm, który każdemu zdarzeniu $E\in {\mathcal E}$, przyporządkuje wartość $\mathcal{T}( E )$ z przeciwdziedziny ${\mathcal {Y}}$, tak by zachować logiczne zależności między zdarzeniami.
Niech wartościami zegara będą pojedyncze liczby ("skalary") naturalne.
W implementacji oznaczać to będzie, że stworzymy zmienną $clock_i$ typu integer
Minimalne własności
Jeżeli lokalne zdarzenie $E_i^k$ w procesie $P_i$ poprzedza lokalnie inne zdarzenie lokalne $E_i^l$, to znacznik czasowy dla $E_i^k$ musi być mniejszy niż $E_i^l$
Wysłanie wiadomości musi być postrzegane jako wcześniejsze niż odebranie tej samej wiadomości, tzn wartości zegara dla wysłania wiadomości muszą być mniejsze niż dla odebrania tejże wiadomości.
Minimalne własności
Jeżeli lokalne zdarzenie $E_i^k$ w procesie $P_i$ poprzedza lokalnie inne zdarzenie lokalne $E_i^l$, to znacznik czasowy dla $E_i^k$ musi być mniejszy niż $E_i^l$
Przy każdym zdarzeniu lokalnym, które uznamy za ważne, $$clock_i = clock_i + step$$
Wysłanie wiadomości musi być postrzegane jako wcześniejsze niż odebranie tej samej wiadomości, tzn wartości zegara dla wysłania wiadomości muszą być mniejsze niż dla odebrania tejże wiadomości.
Minimalne własności
Przy każdym zdarzeniu lokalnym, które uznamy za ważne, $$clock_i = clock_i + step$$
Wysłanie wiadomości musi być postrzegane jako wcześniejsze niż odebranie tej samej wiadomości, tzn wartości zegara dla wysłania wiadomości muszą być mniejsze niż dla odebrania tejże wiadomości.
Każdą wiadomość opatrzymy timestampem (etykietą zegarową), $m.ts$. Wysłanie jest ważnym wydarzeniem, więc zwiększamy $clock_i$ i potem $m.ts = clock_i$. Przy odbiorze w $P_j$ wartość zegara $clock_j$ nie może się cofnąć i nie może być mniejsza od zegara $clock_i$ po wysłaniu.
Minimalne własności
Przy każdym zdarzeniu lokalnym, które uznamy za ważne, $$clock_i = clock_i + step$$
Wysłanie wiadomości musi być postrzegane jako wcześniejsze niż odebranie tej samej wiadomości, tzn wartości zegara dla wysłania wiadomości muszą być mniejsze niż dla odebrania tejże wiadomości.
Każdą wiadomość opatrzymy timestampem (etykietą zegarową), $m.ts$. Wysłanie jest ważnym wydarzeniem, więc zwiększamy $clock_i$ i potem $m.ts = clock_i$. Przy odbiorze w $P_j$ wartość zegara $clock_j$ nie może się cofnąć i nie może być mniejsza od zegara $clock_i$ po wysłaniu.
$$clock_j = max(clock_j, m.ts) + 1$$
Zegary skalarne Lamport
struct message is < blob data , int ts >
local int ~~clock_i~~
Zegary skalarne Lamport
when ~~{P}_i~~ tries to send a message ~~M = \left\langle data, ts \right\rangle~~ to ~~{P}_{j}~~ do
~~clock_i~~ := ~~clock_i + 1~~
~~M.ts~~ := ~~clock_i~~
send ~~M~~ to ~~{P}_j~~
end when
Zegary skalarne Lamport
when at ~~{P}_i~~ arrives a message ~~M = \left\langle data, ts \right\rangle~~ from ~~{P}_{j}~~ do
~~clock_i~~ := ~~max\left(clock_i, M.ts\right) + 1~~
deliver ~~M~~ to ~~{P}_i~~
end when
Przykład zegary
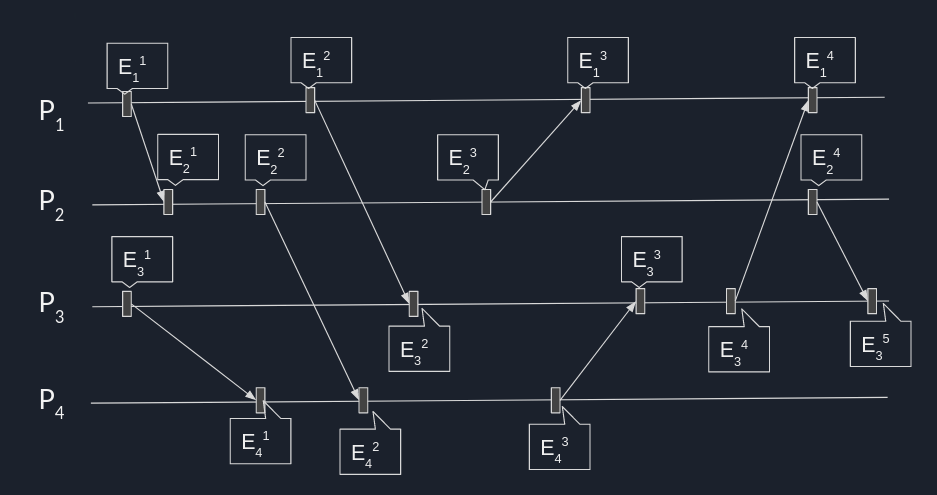
Przykład zegary
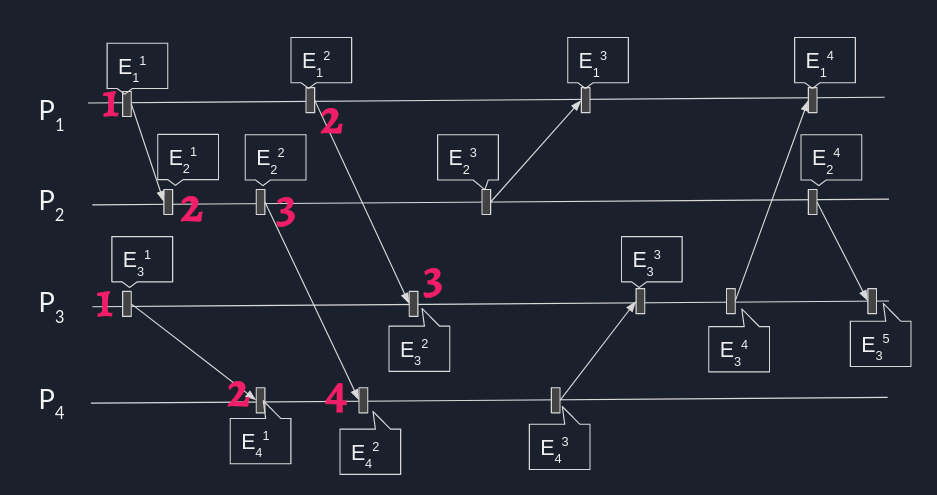
Przykład zegary
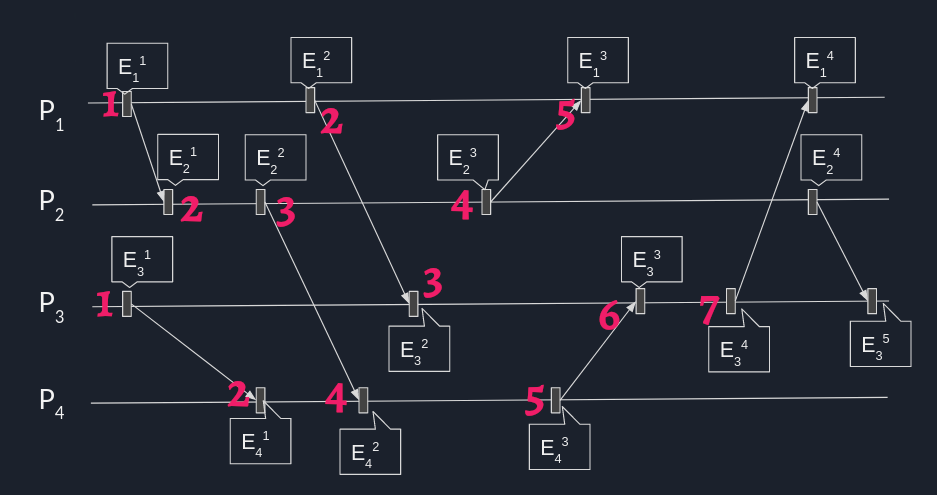
Wartości zegara a relacje między zdarzeniami
$$(E\mapsto E')\Rightarrow ({\mathcal {T}}(E)<{\mathcal {T}}(E')$$ ale $$({\mathcal {T}}(E)<{\mathcal {T}}(E'))\not \Rightarrow (E\mapsto E')$$
Przykład
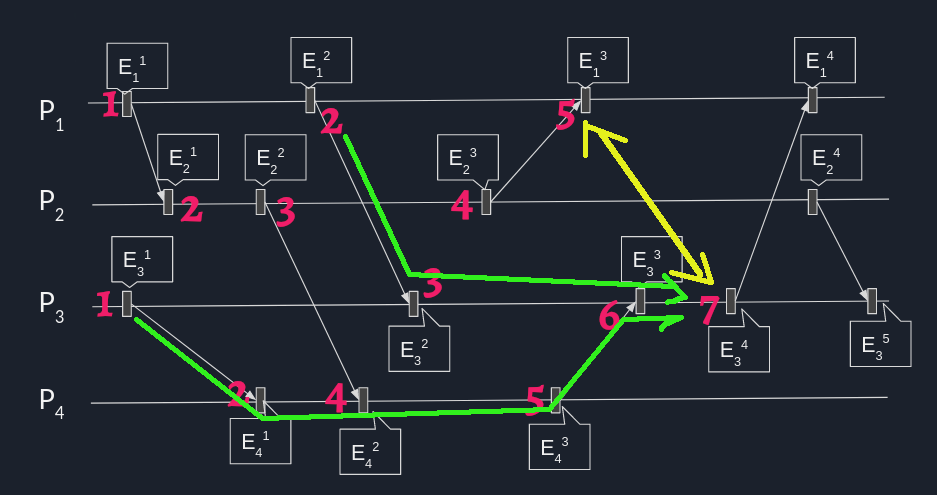
Zalety i wady
- Łatwość w implementacji
- Koszt niezależny od liczby procesów
- Nie pozwala na wnioskowanie o zależnościach między zegarami
Zegary wektorowe
Zegarem logicznym systemu rozproszonego nazywamy pewien abstrakcyjny mechanizm, który każdemu zdarzeniu $E\in {\mathcal E}$, przyporządkuje wartość $\mathcal{T}( E )$ z przeciwdziedziny ${\mathcal {Y}}$, tak by zachować logiczne zależności między zdarzeniami.
Niech wartościami zegara będą wektory liczb naturalnych.
W implementacji oznaczać to będzie, że stworzymy $n$-elementową zmienną $vclock_i$ typu tablicowego integer
Zegary wektorowe
Kiedy w takim razie uznamy, że $vclock_i < vclock_j$?
Zegary wektorowe
Kiedy w takim razie uznamy, że $vclock_i[k] < vclock_j[l]$?
$$vClock_{i}=vClock_{j}\Leftrightarrow \forall k :: vClock_{i}[k]=vClock_{j}[k]$$ $$vClock_{i}\neq vClock_{j}\Leftrightarrow \exists k :: vClock_{i}[k]\neq vClock_{j}[k]$$
Zegary wektorowe
Kiedy w takim razie uznamy, że $vclock_i[k] < vclock_j[l]$?
$$vClock_{i}=vClock_{j}\Leftrightarrow \forall k :: vClock_{i}[k]=vClock_{j}[k]$$ $$vClock_{i}\neq vClock_{j}\Leftrightarrow \exists k :: vClock_{i}[k]\neq vClock_{j}[k]$$
$$ vClock_{i}\leq vClock_{j}\Leftrightarrow \forall k :: vClock_{i}[k]\leq vClock_{j}[k]$$
Zegary wektorowe
$$vClock_{i}=vClock_{j}\Leftrightarrow \forall k :: vClock_{i}[k]=vClock_{j}[k]$$ $$vClock_{i}\neq vClock_{j}\Leftrightarrow \exists k :: vClock_{i}[k]\neq vClock_{j}[k]$$
$$ vClock_{i}\leq vClock_{j}\Leftrightarrow \forall k :: vClock_{i}[k]\leq vClock_{j}[k]$$
$$ vClock_{i} <vClock_{j}\Leftrightarrow \forall k :: vClock_{i}[k]\leq vClock_{j}[k]\land vClock_{i}\neq vClock_{j}$$
Zegary wektorowe
$$vClock_{i}=vClock_{j}\Leftrightarrow \forall k :: vClock_{i}[k]=vClock_{j}[k]$$ $$vClock_{i}\neq vClock_{j}\Leftrightarrow \exists k :: vClock_{i}[k]\neq vClock_{j}[k]$$
$$ vClock_{i}\leq vClock_{j}\Leftrightarrow \forall k :: vClock_{i}[k]\leq vClock_{j}[k]$$
$$ vClock_{i} <vClock_{j}\Leftrightarrow \forall k :: vClock_{i}[k]\leq vClock_{j}[k]\land vClock_{i}\neq vClock_{j}$$
$$vClock_{i}\nless vClock_{j}\Leftrightarrow \neg (\forall k :: vClock_{i}[k]\leq vClock_{j}[k]\land vClock_{i}\neq vClock_{j}$$ $$vClock_{i} || vClock_{j}\Leftrightarrow vClock_{i}\nless vClock_{j}\land vClock_{j}\nless vClock_{i}$$
Zegary wektorowe
| Wektor A | Wektor B |
|---|---|
| 1 | 2 |
| 3 | 3 |
| 2 | 4 |
| 2 | 2 |
Zegary wektorowe
| Wektor A | Wektor B |
|---|---|
| 1 | 2 |
| 4 | 3 |
| 2 | 4 |
| 2 | 2 |
Minimalne własności
Jeżeli lokalne zdarzenie $E_i^k$ w procesie $P_i$ poprzedza lokalnie inne zdarzenie lokalne $E_i^l$, to znacznik czasowy dla $E_i^k$ musi być mniejszy niż $E_i^l$
Wysłanie wiadomości musi być postrzegane jako wcześniejsze niż odebranie tej samej wiadomości, tzn wartości zegara dla wysłania wiadomości muszą być mniejsze niż dla odebrania tejże wiadomości.
Minimalne własności
Jeżeli lokalne zdarzenie $E_i^k$ w procesie $P_i$ poprzedza lokalnie inne zdarzenie lokalne $E_i^l$, to znacznik czasowy dla $E_i^k$ musi być mniejszy niż $E_i^l$
Przy każdym zdarzeniu lokalnym, które uznamy za ważne, $$vclock_i[i] = vclock_i[i] + step$$
Wysłanie wiadomości musi być postrzegane jako wcześniejsze niż odebranie tej samej wiadomości, tzn wartości zegara dla wysłania wiadomości muszą być mniejsze niż dla odebrania tejże wiadomości.
Minimalne własności
Przy każdym zdarzeniu lokalnym, które uznamy za ważne, $$vclock_i[i] = vclock_i[i] + step$$
Wysłanie wiadomości musi być postrzegane jako wcześniejsze niż odebranie tej samej wiadomości, tzn wartości zegara dla wysłania wiadomości muszą być mniejsze niż dla odebrania tejże wiadomości.
Minimalne własności
Przy każdym zdarzeniu lokalnym, które uznamy za ważne, $$vclock_i[i] = vclock_i[i] + step$$
Wysłanie wiadomości musi być postrzegane jako wcześniejsze niż odebranie tej samej wiadomości, tzn wartości zegara dla wysłania wiadomości muszą być mniejsze niż dla odebrania tejże wiadomości.
Przy każdym wysłaniu $vclock_i[i] = vclock_i[i] + step$, a następnie $m.vts = vclock_i$
Minimalne własności
Przy każdym zdarzeniu lokalnym, które uznamy za ważne, $$vclock_i[i] = vclock_i[i] + step$$
Wysłanie wiadomości musi być postrzegane jako wcześniejsze niż odebranie tej samej wiadomości, tzn wartości zegara dla wysłania wiadomości muszą być mniejsze niż dla odebrania tejże wiadomości.
Przy każdym wysłaniu $vclock_i[i] = vclock_i[i] + step$, a następnie $m.vts = vclock_i$
Przy każdym odbiorze $vclock_i[i] = vclock_i[i] + step$, a następnie $$\forall k\neq i : vclock_i[k]=max\left(vclock_i[k], m.vts[k]\right)$$
Zegary skalarne Matterna
struct message is < blob data , int vts >
local int ~~vclock_i[n] := \left\langle 0,0 \ldots 0\right\rangle~~
Zegary skalarne Matterna
when ~~{P}_i~~ tries to send a message ~~M = \left\langle data, vts \right\rangle~~ to ~~{P}_{j}~~ do
~~vclock_i[i]~~ := ~~vclock_i[i] + 1~~
~~M.vts~~ := ~~vclock_i~~
send ~~M~~ to ~~{P}_j~~
end when
Zegary skalarne Matterna
when at ~~{P}_i~~ arrives a message ~~M = \left\langle data, vts \right\rangle~~ from ~~{P}_{j}~~ do
~~vclock_i [i]~~ := ~~vclock_i[i] + 1~~
for all ~~k~~ in ~~0 \ldots n~~ do
if ~~k \neq i~~ then ~~vclock_i[k]~~ := ~~max\left(vclock_i[k], M.vts[k]\right)~~
end for
deliver ~~M~~ to ~~{P}_i~~
end when
Przykład zegary

Przykład zegary
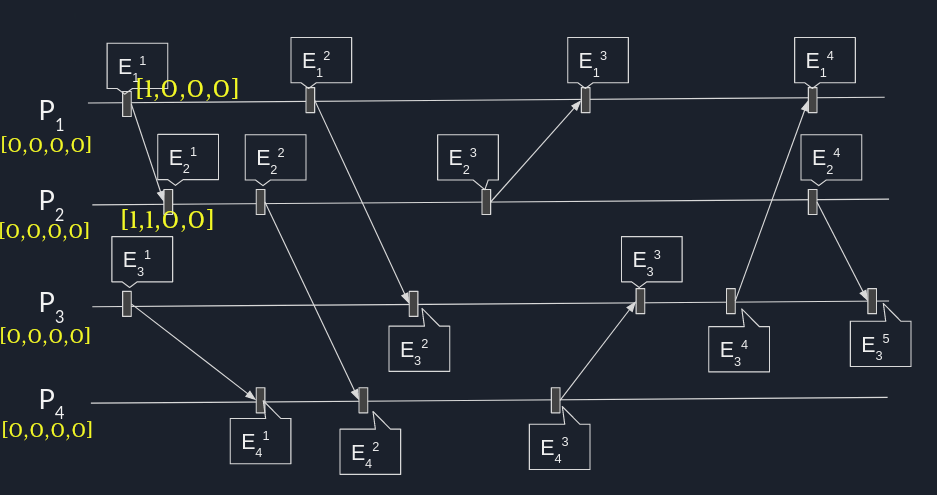
Wartości zegara wektorowego a relacje między zdarzeniami
$$(E\mapsto E')\iff ({\mathcal {T}}(E)<{\mathcal {T}}(E')$$
$$(E || E')\iff ({\mathcal {T}}(E) || {\mathcal {T}}(E')$$
Wady i zalety
- Pozwala wnioskować o zależnościach między zdarzeniami
- Nieco bardziej skomplikowana implementacja
- Rozmiar rośnie z liczbą procesów
Poprawność algorytmów
- Bezpieczeństwo: to, czego nie chcemy, nigdy się nie wydarzy
- Postęp, żywotność: to, czego chcemy, ostatecznie się wydarzy
Złożoność czasowa i komunikacyjna
Mój algorytm jest lepszy niż Twój!
Implementacja, uruchomienie programu i pomierzenie czasów rzeczywistych to ZUUUUOOO:
- Mierzymy jakość algorytmu, czy umiejętności programisty? Nb: ten sam programista może mieć idiosynkrazje powodujące, że jakieś algorytmy implementuje lepiej, bo je lepiej np. zrozumie
- Co, jeżeli jakiś mały szczegół wpływa na wyniki testów? (por. wpływ opcji środowiskowych na wyników testów szybkości kompilacji gcc)
- A może porównujemy kompilatory? A może języki?
- A co, jeżeli za rok wejdzie w życie nowa optymalizacja kompilatora, przyjdzie nowy programista, zmieni się jakiś szczegół środowiska?
Wymagania
Chcemy miarę teoretyczną, niezależną od języka, kompilatorów, środowiska.
Miara ma pozwalać na szybkie porównywanie mocnych i silnych stron algorytmów.
Równocześnie będziemy mieli świadomość, że miara ta to złożoność teoretyczna, tj dla określonego środowiska lub dla konkretnych wymagań algorytm teoretycznie gorszy może okazać się w rzeczywistości bardziej pożądany.
Specyfika środowiska rozproszonego
Interesują nas algorytmy wymagające współpracy między procesami rozproszonymi rozwiązujące problemy inne, niż wymagające np. dużej mocy obliczeniowej albo przepustowości. To jest: chodzi nam np. o dostęp do sekcji krytycznej, rozgłaszanie itd.
Pozostaje rozważyć, co właściwie i jak chcemy liczyć.
Specyfika środowiska rozproszonego
- Ile cykli zegarowych zajmuje przesłanie wiadomości w sieci lokalnej?
- Jakie będą najmniejsze i największe wiadomości?
- Jakie są różnice w przesłaniu w wiadomości 32 bajtów i 512 bajtów?
- Czy jest sens zajmować się konkretnymi czasami przesłania wiadomości, skoro one zależą od technologii?
Założenia
- Pomijamy czasy przetwarzania lokalnego
- Czasy przesłania każdej wiadomości liczymy jako jedną turę
Pamiętamy : to założenia mające sens dla algorytmów tego rodzaju, jakie będziemy rozważać!
Złożoność czasowa i komunikacyjna
- Złożoność komunikacyjna (pakietowa): ile przesyłamy wiadomości?
- Złożoność czasowa: ile tur nam to zajmie?
Dygresja: kiedy nasz algorytm się kończy?
- Czy algorytm się kończy, kiedy osiąga efekt, czy dopiero wtedy, kiedy przestaje rozgłaszać wiadomości (wygaszanie)?
- Czy wszystkie fazy bierzemy pod uwagę?
- Czy bierzemy pod uwagę interakcje między różnymi przebiegami tego samego algorytmu, uruchomionymi przez różne procesy?