Przetwarzanie rozproszone

Ten nudny wykład z definicjami

dr inż. Arkadiusz Danilecki

Plan wykładu

Po co?
Czym się zajmujemy na przetwarzaniu rozproszonym?
Po co to robimy?
Przykłady
Definicje

Po co?

Informatyka jest nauką ścisłą i wymaga ścisłych definicji, by uniknąć dwuznaczności obecnych w języku potocznym

Musimy ustalić wspólny język, by się rozumieć

No worries! Na potrzeby wykładu uprościmy wszystko jak tylko się da, rezygnując z części formalizmów.

Definicje

Rozproszony system informatyczny obejmuje środowisko przetwarzania rozproszonego (węzły, łącza) oraz procesy rozproszone (zbiory procesów sekwencyjnych realizujących wspólne cele przetwarzania).

Definicje

Środowisko przetwarzania rozproszonego jest zbiorem $\mathcal{N}$ autonomicznych jednostek przetwarzających (węzłów), zintegrowanych siecią komunikacyjną (środowiskiem komunikacyjnym, łączami komunikacyjnymi, łączami transmisyjnymi).

Definicje

Jednostki przetwarzające realizują przetwarzanie z prędkością narzucaną przez lokalne zegary. Jeżeli zegary te są niezależne, to mówimy, że węzły działają asynchronicznie. Jeżeli natomiast zegary te są zsynchronizowane lub istnieje wspólny zegar globalny dla wszystkich węzłów, to mówimy, że węzły działają synchronicznie.

Definicje

Jednostka przetwarzająca a $N_i \in \mathcal{N}$ (węzeł) jest elementem środowiska przetwarzania rozproszonego obejmującym:

procesor,
pamięć lokalną,
interfejs komunikacyjny.

Procesor wykonuje automatycznie program zapisany w pamięci lokalnej, gdzie pamiętane są również dane. Interfejs komunikacyjny umożliwia węzłom dostęp do łączy i tym samym wzajemną wymianę informacji - komunikatów (ang. message passing, message exchange) oraz komunikację z użytkownikiem.

Definicje

Jednostka przetwarzająca a $N_i \in \mathcal{N}$ (węzeł) jest elementem środowiska przetwarzania rozproszonego obejmującym:

procesor,
pamięć lokalną,
interfejs komunikacyjny.

Definicje

W środowisku przetwarzania rozproszonego, komunikacja między węzłami możliwa jest tylko przez transmisję pakietów informacji (wiadomości, komunikatów) łączami komunikacyjnymi.

Definicje

W środowisku przetwarzania rozproszonego, komunikacja między węzłami możliwa jest tylko przez transmisję pakietów informacji (wiadomości, komunikatów) łączami komunikacyjnymi.

Łącze komunikacyjne jest elementem pozwalającym na transmisję informacji między interfejsami komunikacyjnymi odległych węzłów. Wyróżnia się łącza jedno i dwukierunkowe. Łącza mogą być FIFO/nonFIFO, lub oferować dodatkowe gwarancje jeżeli chodzi o niezawodność.

Definicje

Procesem rozproszonym $\Pi$ (przetwarzaniem rozproszonym) nazywamy współbieżne i skoordynowane (ang. concurrent and coordinated) wykonanie w środowisku rozproszonym zbioru $\mathcal {P}$ procesów sekwencyjnych $P_1 , P_2 , P_3 , \ldots, P_n$ współdziałających w realizacji wspólnego celu przetwarzania.

Definicje

Nieformalnie, każdy proces sekwencyjny (zadanie) jest działaniem wynikającym z wykonywania w pewnym środowisku (kontekście) programu sekwencyjnego (algorytmu sekwencyjnego), który składa się z ciągu operacji (instrukcji, wyrażeń) atomowych (nieprzerywalnych).

Definicje

Kanał jest obiektem (zmienną) skojarzonym z uporządkowaną parą procesów $\left\langle P_{i},P_{j}\right\rangle $, modelującym jednokierunkowe łącze transmisyjne.

Definicje

Kanał jest obiektem (zmienną) skojarzonym z uporządkowaną parą procesów $\left\langle P_{i},P_{j}\right\rangle $, modelującym jednokierunkowe łącze transmisyjne.

Kanał skojarzony z parą procesów $ \left\langle P_{i},P_{j}\right\rangle $, oznaczamy przez $C_{i,j} \in \mathcal{C}$ oraz nazywamy kanałem incydentnym z procesem $P_{i}$ i z procesem $P_{j}$. Ponadto, kanał $C_{i,j}$ nazywamy kanałem wyjściowym procesu $P_{i}$ oraz kanałem wejściowym procesu $P_j$.

Definicje

Każdy proces $P_i$ posiada stan, który w chwili $t$ oznaczać będziemy jako $S_i(t)$.

Zamiast zależności od czasu możemy używać oznaczenia $S_i^k$ na oznaczenie $k$-tego stanu procesu $P_i$.

Dla uproszczenia zapisu, gdy zależność od czasu jest oczywista, będziemy ją pomijać i pisać po prostu $S_i$.

Definicje

Każdy proces $P_i$ posiada stan, który w chwili $t$ oznaczać będziemy jako $S_i(t)$.

Zamiast zależności od czasu możemy używać oznaczenia $S_i^k$ na oznaczenie $k$-tego stanu procesu $P_i$.

Dla uproszczenia zapisu, gdy zależność od czasu jest oczywista, będziemy ją pomijać i pisać po prostu $S_i$.

Analogicznie, stan całego procesu rozproszonego $\Pi$ w chwili czasu globalnego $\tau$ oznaczymy jako $\Sigma(\tau)$, Dla uproszczenia zapisu, gdy zależność od czasu jest oczywista, będziemy ją pomijać i pisać po prostu $\Sigma$.

Definicje

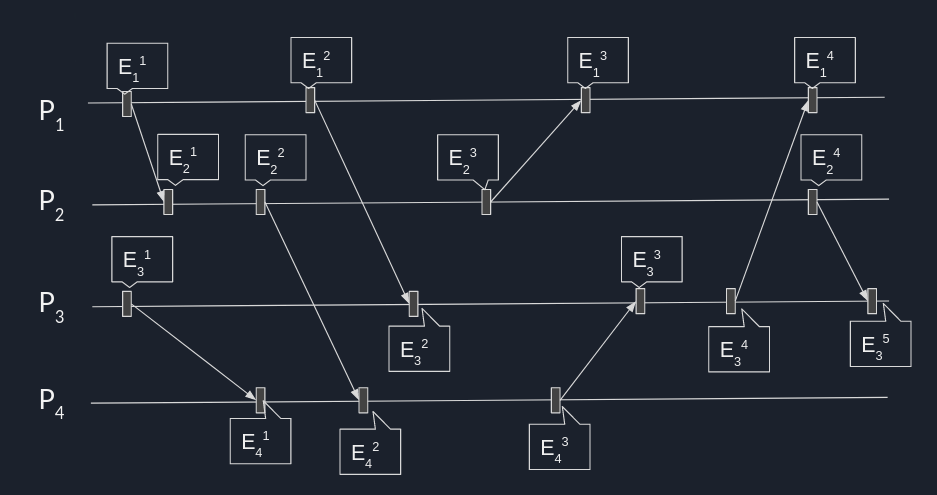
Procesy wykonując kroki algorytmu generują zdarzenia. Dla procesu $P_i$, jego $k$-te zdarzania zapiszemy jako $E_i^k$. Zbiór wszystkich możliwych zdarzeń oznaczymy jako $\mathcal{E}$.

Rozróżniamy zdarzenia wewnętrzne oraz komunikacyjne

Podsumowanie oznaczeń

$\Pi , \Sigma, \tau$ - pojęcia odnoszące się do całego systemu

$P_i, S_i, E_i, t$ - pojęcia odnoszące się do $i$-tego elementu systemu (procesu sekwencyjnego)

$\mathcal{P}, \mathcal{S}, \mathcal{T}, \mathcal{E}$ - zbiory elementów

Determinizm przetwarzania

W przetwarzaniu rozproszonym inherentny jest pewien niedeterminizm wynikający choćby z opóźnień komunikacyjnych

W szczególności, interesuje nas klasa przetwarzania quasi-deterministycznego albo piecewise deterministic w których niedeterminizm wynika tylko i wyłącznie ze zdarzeń komunikacyjnych

Wykonanie i historia wykonania

Niech wykonanie procesu $\Pi$ oznacza naprzemienny ciąg $$E^0, \Sigma^0, E^1, \Sigma^1 \ldots E^n, \Sigma^n$$

Ciąg samych zdarzeń z powyższego nazwiemy historią wykonania

Relacja poprzedzania zdarzeń

Zbiór zdarzeń $\mathcal{E}_{i}$ procesu $P_i$ jest w pełni uporządkowany, według kolejności ich występowania w czasie lokalnym t.

Wprowadzimy teraz relację $\mapsto$ - relację poprzedzania (ang. happen before, causal precedence, happened before) zdefiniowaną na zbiorze $\mathcal{E}$ w następujący sposób:

Relacja poprzedzania zdarzeń

Wprowadzimy teraz relację $\mapsto$ - relację poprzedzania (ang. happen before, causal precedence, happened before) zdefiniowaną na zbiorze $\mathcal{E}$ w następujący sposób:

$E_{i}^{k}\mapsto E_{j}^{l}\iff { \begin{cases} {\mbox{1)}}i=j\land k <l, ( {\mbox{ co zapisujemy }} E_i^k \mapsto_i E_j^l ){\mbox{ lub }}\\ {\mbox{2)}}i\neq j{\mbox{ oraz }}E_{i}^{k}{\mbox{ jest zdarzeniem wysłania wiadomości }}M,\\ {\mbox{ a zdarzenie }}E_{j}^{l}{\mbox{ jest zdarzeniem odbioru tej samej wiadomości, lub }}\\ {\mbox{3)}}{\mbox{ istnieje sekwencja zdarzeń }}E^{0},E^{1},E^{2},\ldots ,E^{s}{\mbox{, taka że }}\\E^{0}=E_{i}^{k},E^{s}=E_{j}^{l}{\mbox{ i dla każdej pary }}\left\langle E^{u},E^{u+1}\right\rangle \\{\mbox{ gdzie }}0\leq u\leq s-1{\mbox{, zachodzi 1) albo 2).}}\end{cases}}$

Relacja poprzedzania jest antysymetryczna i przechodnia, a więc jest relacją częściowego porządku.

Relacja poprzedzania stanów

Analogicznie można wprowadzić relację poprzedzania stanów; Jeżeli $E^k \mapsto E^l$, to $S^{k-1} \mapsto S^{l}$

Ponieważ znając historię można wyznaczyć stan globalny, będziemy często pisać i mówić o "zdarzeniach należących do stanu"

Zdarzenia przyczynowo zależne i niezależne

Kod


				    when ~~{P}_i~~ tries to send ~~M = \left\langle data \right\rangle~~ to ~~{P}_{j}~~ do
				       ~~M~~ := ~~M \cup \left \langle .data := x   \right\rangle ~~
				       send ~~M~~ to ~~{P}_j~~
				    end when

Kod


				    when message ~~M = \left\langle data \right\rangle~~ arrives at ~~{P}_i~~ from ~~{P}_{j}~~ do
				       ~~x~~ := ~~M.data~~
				       deliver ~~M~~ 
				    end when