Funktory
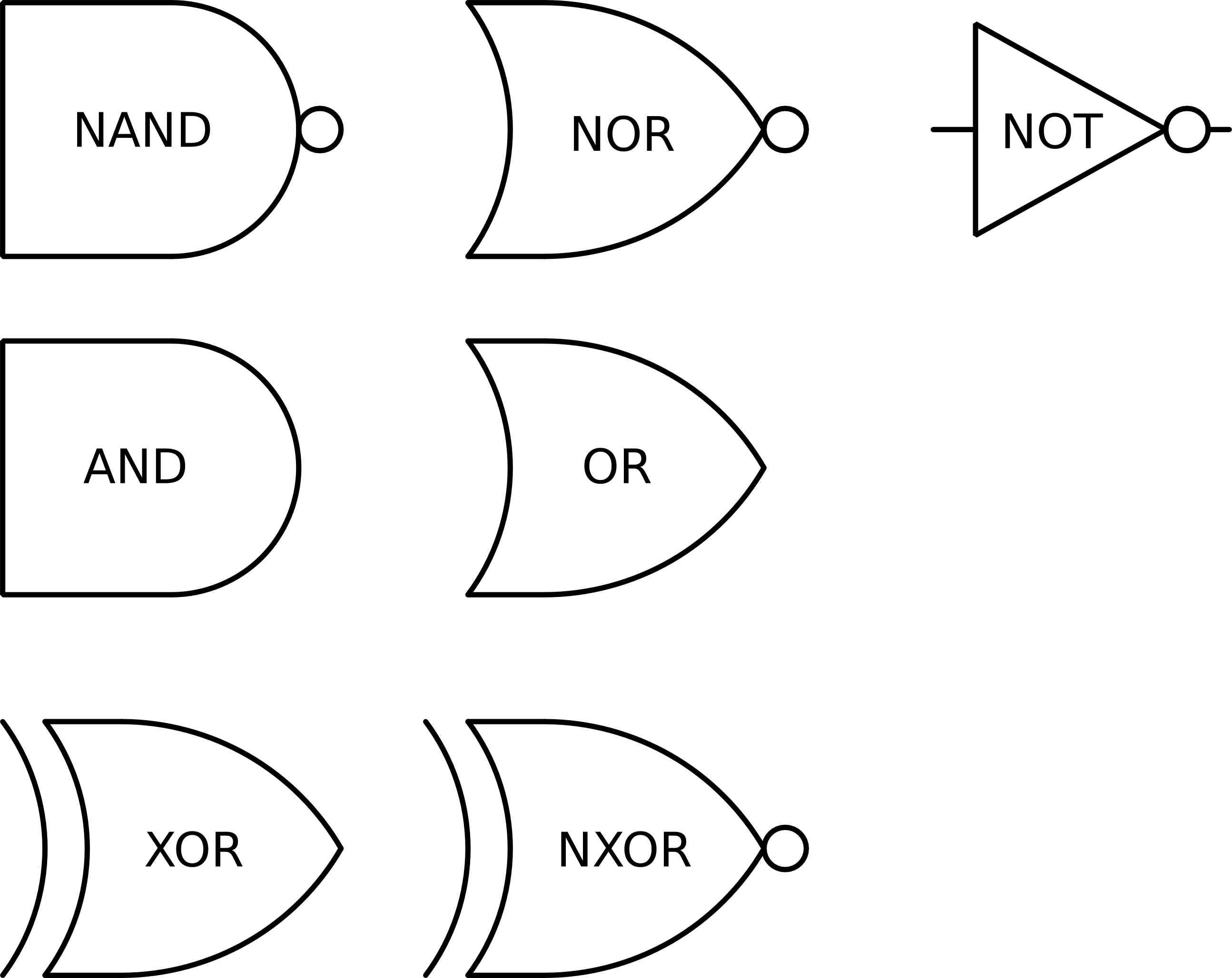
- W ogólności uznaje się, że bramki (poza NOT) mogą mieć dowolną liczbę wejść i ich słowny opis działania jest następujący:
- AND - 1 jeśli wszystkie wejścia były równe 1
- OR - 1 jeśli co najmniej jedno wejście było równe 1
- XOR - 1 jeśli nieparzysta liczba wejść była równa 1
- NAND, NOR, NXOR - tak jak AND, OR i XOR odpowiednio, ale negując wynik
- Bramki NOT nie trzeba stosować bezpośrednio. Dozwolone jest umieszczenie "kółeczka" przy wejściu, które ma zostać zanegowane
Tablice Karnaugh
- Aby znaleźć minimalną funkcję w algebrze Boole'a, która odpowiada zadanej tabelce prawdy, należy skonstruować tabelkę Karnaugh.
- Wiersze i kolumny mają etykiety odpowiadające zmiennym logicznym:
- dla dwóch zmiennych:
| A\B | 0 | 1 |
| 0 | ... | ... |
| 1 | ... | ... |
- dla trzech zmiennych:
| AB\C | 0 | 1 |
| 00 | ... | ... |
| 01 | ... | ... |
| 11 | ... | ... |
| 10 | ... | ... |
- dla czterech zmiennych:
| AB\CD | 00 | 01 | 11 | 10 |
| 00 | ... | ... | ... | ... |
| 01 | ... | ... | ... | ... |
| 11 | ... | ... | ... | ... |
| 10 | ... | ... | ... | ... |
- Tabelkę Karnaugh wypełnia się wg tabelki prawdy, ale uwaga na zastosowany kod Graya (w tabelce Karnaugh jest kolejność 00, 01, 11, 10)
- Rozwiązanie "dla jedynek". Szukamy w tabelce skupisk jedynek, które spełniają pewne wymagania:
- w skupisku musi być liczba jedynek równa 1, 2, 4, 8 lub 16 (potęga dwójki),
- muszą one ze sobą sąsiadować tzn. tworzyć linię lub prostokąt,
- sąsiedztwo to określone jest także dla brzegowych miejsc tzn. przykładowo jedynki z pierwszej kolumny mogą tworzyć skupisko z jedynkami z ostatniej kolumny.
- Należy określić takie skupiska, żeby były jak największe i żeby ostatecznie każda jedynka do któregoś należała. Aby zapewnić pierwszą cechę, dopuszczalne jest by pewne jedynki należały do kilku skupisk.
- Przykładowa tabelka:
| AB\C | 0 | 1 |
| 00 | 0 | 1 |
| 01 | 1 | 1 |
| 11 | 1 | 0 |
| 10 | 0 | 1 |
- Znalezione skupiska: (nie ma żadnych 8- ani 4-elementowych - od nich należało rozpocząć szukanie)
| AB\C | 0 | 1 |
| 00 | 0 | 1 |
| 01 | 1 | 1 |
| 11 | 1 | 0 |
| 10 | 0 | 1 |
| AB\C | 0 | 1 |
| 00 | 0 | 1 |
| 01 | 1 | 1 |
| 11 | 1 | 0 |
| 10 | 0 | 1 |
| AB\C | 0 | 1 |
| 00 | 0 | 1 |
| 01 | 1 | 1 |
| 11 | 1 | 0 |
| 10 | 0 | 1 |
(tutaj właśnie sąsiedztwo jest oparte na brzegowych wartościach)
- Dla każdego skupiska szukamy teraz funkcji, która je opisuje. Patrząc na wiersze i kolumny, szukamy które wejściowe zmienne logiczne mają dla danego skupiska stałą wartość. Spójrzmy na pierwsze skupisko - widać, że A jest dla niego zawsze równe 0, B zmienia się między 0 i 1, C jest zawsze równe 1. Pomijamy zatem B i dla tego skupiska zapisujemy funkcję:
~A*C - Analogicznie dla kolejnych skupisk otrzymujemy:
B*~Coraz~B*C - Poszukiwana funkcja dla pierwotnych danych to dysjunkcja znalezionych funkcji dla skupisk:
f(A, B, C) = (~A*C) + (B*~C) + (~B*C)
- Rozwiązanie "dla zer" jest analogiczne. Różnica polega na tym, że szukamy skupisk zer i po połączeniu znakami dysjunkcji wszystkich funkcji cząstkowych, otrzymujemy zanegowaną postać funkcji pierwotnej. Zobaczmy to na przykładzie dla tych samych danych:
| AB\C | 0 | 1 |
| 00 | 0 | 1 |
| 01 | 1 | 1 |
| 11 | 1 | 0 |
| 10 | 0 | 1 |
| AB\C | 0 | 1 |
| 00 | 0 | 1 |
| 01 | 1 | 1 |
| 11 | 1 | 0 |
| 10 | 0 | 1 |
- Tym razem są dwa skupiska. Jedno z nich jest tylko 1-elementowe, ale musimy je wziąć pod uwagę, bo nie może zostać pominięty żaden element.
- Nasza funkcja wynikowa to:
~f(A, B, C) = (~B*~C) + A*B*C
- Z praw de Morgana można otrzymać oczywiście postać niezanegowaną postać funkcji:
~[~f(A, B, C)] = f(A, B, C)
= ~[(~B*~C) + A*B*C]
= ~(~B*~C) * ~(A*B*C)
= (B + C) * (~A + ~B + ~C) - Rozwiązania "dla jedynek" i "dla zer" są sobie równoważne. Jak widać z powyższego przykładu, wybór metody czasem prowadzi do różnej liczby kroków do wykonania.
Operacje bitowe w języku C
- Operator AND:
&int x = 7, y = 10;
printf("%d\n", x & y); // 2
/*
* 0111b = 7
* 1010b = 10
* -------
* & 0010b = 2
*/ - Operator OR:
|int x = 7, y = 10;
printf("%d\n", x | y); // 15
/*
* 0111b = 7
* 1010b = 10
* -------
* | 1111b = 15
*/ - Operator XOR:
^int x = 7, y = 10;
printf("%d\n", x ^ y); // 2
/*
* 0111b = 7
* 1010b = 10
* -------
* ^ 1101b = 13
*/ - Operator NOT:
~int x = 0;
printf("%d\n", ~x); // -1
/*
* 0000b = 0
* -------
* ~ 1111b = -1
*/ - Operator przesunięcia bitowego w lewo:
<<int x = 7, y = 1;
printf("%d\n", x << y); // 28
/*
* 0111b = 7
* -----------
* << 1 1110b = 14
*/ - Operator przesunięcia bitowego w prawo:
>>int x = 7, y = 1;
printf("%d\n", x >> y); // 3
/*
* 0111b = 7
* -----------
* >> 1 0011b = 3
*/
Uwaga, zwróć uwagę na różnicę pomiędzy & i &&
int a = 1, b = 2;
if (a && b) {
printf("TO SIE POJAWI\n");
}
if (a & b) {
printf("TO SIE NIE POJAWI\n");
}
if (a && b) {
printf("TO SIE POJAWI\n");
}
if (a & b) {
printf("TO SIE NIE POJAWI\n");
}