Definicje podstawowych pojęć

Istota teorii zbiorów rozmytych       Pojęcie zbioru rozmytego        Zasada rozszerzania Zadeha         Zmienna lingwistyczna

Istota teorii zbiorów rozmytych

Informacja jaką akceptują metody oparte na konwencjonalnej matematyce musi być precyzyjna, np. prędkość samochodu v = 111 km/h. Informację taką można przedstawić graficznie z użyciem tzw. singletona.

Rys. Wizualizacja precyzyjnego pomiaru prędkości.

Człowiek potrafi ocenić prędkość samochodu stosując pojęcia takie jak prędkość mała, średnia, duża. Te nieprecyzyjne oceny można również przedstawić graficznie.

Rys. Wizualizacja nieprecyzyjnej, zgrubnej oceny prędkości.

 Funkcje “mała”, “średnia”, “duża” określane mianem funkcji przynależności informują, czy dana, precyzyjna wartość prędkości jest zaliczana do prędkości małej, średniej, czy dużej. Człowiek obserwujący samochód jadący z prędkością v = 111 km/h nie potrafi precyzyjnie ocenić jego prędkości. Może ją jednak ocenić zgrubnie jako dużą. Informację taką można nazwać ziarnem informacji. 

Informacja uzyskiwana od ludzi jest zwykle mniej precyzyjna (duża ziarnistość), informacja z urządzeń pomiarowych bardziej precyzyjna (mała ziarnistość). Ziarnistość informacji określona jest przez szerokość ziarna. I tak ziarno "średnia" może mieć różne szerokości, zależnie od łącznej ilości ziaren informacji, jakie stosuje człowiek. Zmniejszając ziarnistość informacji dochodzimy w granicy do ziarna o nieskończenie małej szerokości zwanego singletonem i reprezentującego informację precyzyjną.

Informacja o skończonej, większej od zera szerokości ziarna nazwana została informacją rozmytą. Dział matematyki operujący taką informacją teorią zbiorów rozmytych. Jej najważniejszym elementem jest logika rozmyta stosowana do modelowania i sterowania rozmytego.

Pojęcie zbioru rozmytego

Celem zbioru (konwencjonalnego) w matematyce jest właściwie określenie pewnego pojęcia. Na przykład pojęcie “liczby całkowite większe lub równe 3 i mniejsze lub równe 10” można jednoznacznie przedstawić w postaci następującego zbioru {x Î I : 3 ≤ x ≤ 10} = {3,4,5,6,7,8,9,10}, gdzie I jest zbiorem liczb całkowitych.

Zbiór konwencjonalny; powiedzmy A, można utożsamić z jego funkcją charakterystyczną

φ_A: X → {0,1}

która każdemu elementowi x przestrzeni rozważań X = {x} (w naszym przykładzie X = I, tzn. jest zbiorem liczb całkowitych) przypisuje liczbę φ(x) Î {0, l}, taką że φ_A(x) = 0 oznacza, iż dany x Î X nie należy do zbioru A, a φ_A (x) = l oznacza, iż dany x Î X należy do zbioru A.

Łatwo jednak zauważyć, że napotyka się na poważne trudności, gdy chce się przedstawić w sposób formalny (za pomocą zbioru) pojęcia nieostre typu “liczby całkowite, które są mniej więcej równe 6" - źródłem nieprecyzyjności (rozmytości) jest tu oczywiście określenie mniej więcej.

Elementy zbioru rozmytego mogą do niego należeć do pewnego stopnia: od pełnej przynależności do pełnej nie przynależności, przez wszystkie stopnie pośrednie.

Jeżeli teraz rozpatrzymy zbiór rozmyty “liczb całkowitych mniej więcej równych 6", to x = 6 na pewno należy do takiego zbioru rozmytego, a zatem μ_A (6) = 1, liczby 5 i 7 należą do niego “prawie na pewno", a zatem μ_A (5) i μ_A (7) są bliskie l,
 a im bardziej liczba różni się od 6, tym mniejsze jest μ_A (.). W końcu, liczby poniżej 2 i powyżej 10 nie należą do takiego zbioru rozmytego, a więc dla nich μ_A (.) = 0.

Rys. Funkcja przynależności zbioru rozmytego “liczby całkowite mniej więcej równe 6”.

W praktyce funkcję przynależności zbioru rozmytego przyjmuje się zazwyczaj w postaci kawałkami liniowej, jak to pokazano na rysunku poniżej dla takiego samego zbioru rozmytego, jak na rysunku powyżej, tzn. “liczby całkowite mniej więcej równe 6". W takim przypadku do określenia funkcji przynależności potrzeba tylko czterech punktów: a, b, c i d; na rysunku poniżej są one równe: a = 2, b = 5, c = 7 i d = 10.

Rys. Kawałkami liniowa funkcja przynależności zbioru rozmytego “liczby całkowite mniej więcej równe 6”.

 Zauważmy, że w zbiorze rozmytym przejście od przynależności do nie przynależności jest stopniowe, a nie skokowe. Pojęcie zbioru rozmytego daje nam więc to, co jest nam potrzebne do określania pojęć nieostrych. 

Zasada rozszerzania Zadeha

Arytmetyka ta definiuje podstawowe operacje matematyczne na liczbach rozmytych przez rozszerzenie tych operacji z liczb nierozmytych. Sposób ich rozszerzania podaje tzw. zasada rozszerzania Zadeha.

Dany jest system nierozmyty typu jedno wejście / jedno wyjście realizujący odwzorowanie f przestrzeni wejścia X w przestrzeni wyjścia Y. Jeżeli A jest zbiorem rozmytym zdefiniowanym w przestrzeni X to odwzorowaniem f(A) tego zbioru w przestrzeni wyjścia Y jest, zgodnie z zasadą rozszerzania, zbiór B = f(A) określony wzorem, gdzie znak Ú oznacza operator LUB.

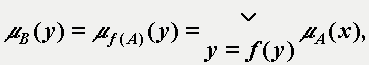      xÎ X, yÎ Y

 W przypadku wielu systemów rzeczywistych wielkości wejściowe i wyjściowe mogą być wyrażone przy pomocy liczb rzeczywistych (np. napięcie i natężenie prądu), dlatego dalej przestrzenie rozważań X,Y będą przestrzeniami liczb rzeczywistych R.

Zmienna lingwistyczna

Zmienną lingwistyczną jest ta wielkość wejściowa, wyjściowa bądź zmienna stanu, którą zamierzamy ocenić stosując oceny lingwistyczne, zwane wartościami lingwistycznymi, np. prędkość statku, napięcie, temperatura. W praktycznych zastosowaniach zmienne lingwistyczne oceniane są nie tylko przy pomocy wartości lingwistycznych ale także liczb rozmytych, czyli w sposób mieszany.

Wartość lingwistyczna jest słowną oceną wielkości lingwistycznej, np. bardzo duży, ładny, brzydki, przyjemny, prawdziwy, nieprawdziwy.

Wartości lingwistyczne występują w modelach wraz ze zmiennymi lingwistycznymi których dotyczą, np. wysokie ciśnienie powietrza, silny strumień wody, młody wiek, prawdziwa informacja, fałszywa informacja.

Rys.  Przykład precyzyjnej oceny zmiennej, opisanej dużą ilością informacji.

Informacja przedstawiona precyzyjnie (w sposób nierozmyty) na wykresie może być uogólniona przy pomocy liczby rzeczywistej: