New Page 1

New Page 1

Symulator sterowania wybranym obiektem przy pomocy sieci neuronowych.

Program realizuje symulację sterowania obiektem przy pomocy sieci neuronowych. Umożliwia on symulacyjne badanie jakości regulacji, użytkownik ma możliwość wpływania na podstawowe parametry sieci neuronowych jak współczynnik szybkości uczenia sieci. może również definiować współczynniki badanego obiektu, który jest opisany równaniem typu ARMA.

Struktura sieci i algorytm sterowania zastosowane w rozwiązaniu

Ponieważ system miał działać w czasie rzeczywistym dlatego odrzucone zostały modele z neuronami w warstwach ukrytych i zaimplementowano najprostszą sieć dwuwarstwową z jednym neuronem wyjściowym.

Model układu sterującego jest przedstawiony na poniższym rysunku:

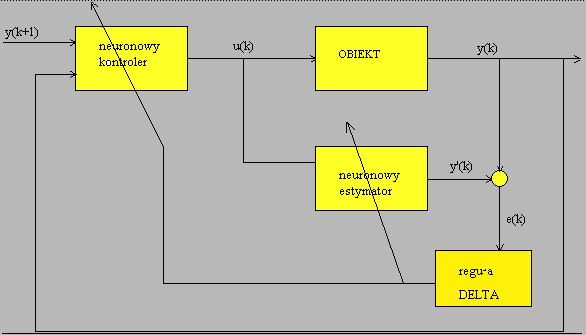
Aby można było zaimplementować powyższy schemat, trzeba przyjąć, że obiekt jest opisany następującym równaniem ARMA (klasyczne równanie dyskretne):

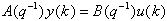
A(q^-1) oraz B(q^-1) są wielomianami zdefiniowanymi następująco:

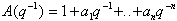
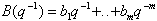
gdzie:
;

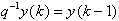Trzeba tu założyć co następuje :

             1) znane są górne granice n i m ,
               2) B(q-1) jest wielomianem stabilnym,
               3) współczynnik b1 jest różny od zera.

Warunek pierwszy jest konieczny aby można było wyestymować parametry badanego obiektu. Warunek drugi musi być spełniony aby otrzymać stabilną pętlę sterowania sterownika neuronowego, trzecie założenie musi być spełnione aby móc skonstruować neuronowy sterownik.

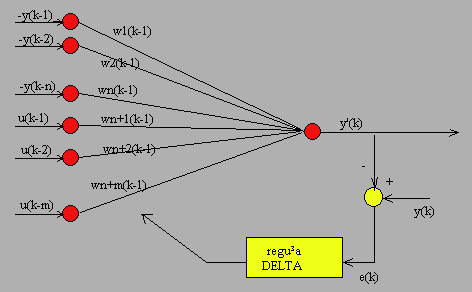
Estymatorem jest w tym przypadku dwuwarstwowa liniowa sieć neuronowa składająca się z n+m wejść. Podajemy na nią takie same sygnały jak na sterowany obiekt. Sieć ta uczy się dynamiki badanego obiektu.

Neuronowy estymator

Wektor wag sieci neuronowej ma następującą postać:

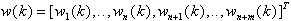
Wektor ten jest uaktualniany zgodnie z regułą Widrowa-Hoffa:

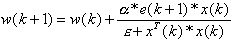
gdzie:

- a (0,2) i jest współczynnikiem uczenia sieci,
- e powinien dążyć do zera ( ma uchronić nas przed dzieleniem przez zero gdy iloczyn

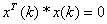
Tak jak to jest zaprezentowane na powyższym rysunku, sygnał błędu predykcji e(k) jest różnicą pomiędzy rzeczywistą odpowiedzią obiektu a wyestymowaną wartością 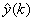otrzymaną z neuronowego estymatora. Wartość wyestymowanego sygnału jest obliczana ze wzoru:

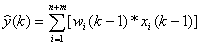
Sterownik neuronowy podobnie jak estymator składa się z dwóch warstw neuronów z n+m warstwami wejściowymi i 1 warstwą wyjściową.

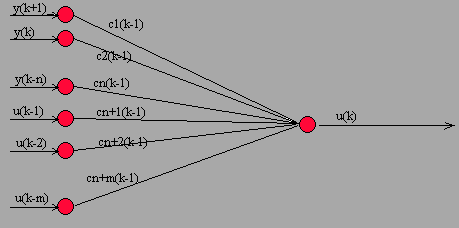
Wektor wejściowy sterownika jest zdefiniowany następująco :

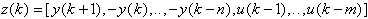
a wektor wag sterownika definiuje się następująco :

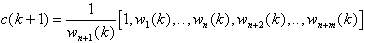
Sygnał sterujący u(k) jest sumą iloczynów następującego wyrażenia :

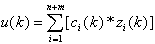
3 Algorytm sterowania

Sekwencja sterowania obiektem przedstawia się następująco:

1. Zmierz y(k+1) oraz y(k);
   2. Przy pomocy estymatora oblicz 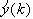korzystając ze starych wag wi(k-1);
   3. Oblicz e(k)=y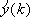(k) - i przy pomocy reguły DELTA nowe wagi wi(k);
   4. Zmień wagi ci(k);
   5. Przy pomocy sterownika oblicz nowy sygnał sterujący u(k).

Program symulacyjny oraz moduł do sterowania silnikiem krokowym zastał napisany w języku Turbo Pascal 7.0 w środowisku Turbo Vision.

Opis programu

Opis powiązań między modułami

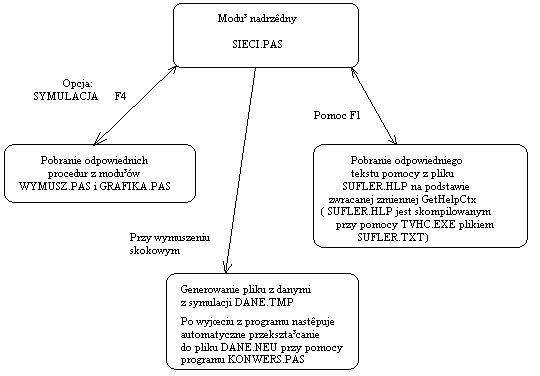
Zasadniczy program składa się z kilku modułów. Modułem nadrzędnym jest moduł sieci.pas. Z jego poziomu wywoływane są następujące moduły ( w odpowiedzi na działania użytkownika ):

grafika.pas - moduł ten zawiera procedury obsługujące ekran graficzny podczas wyświetlania efektów symulacji ( wyświetla ramki, napisy, komunikaty itp. w trybie graficznym);

wymusz.pas - w module tym są zdefiniowane poszczególne sygnały wymuszające podawane na badany obiekt; Parametrem przekazywanym do tego modułu jest numer wymuszenia (np. 1 - skok jednostkowy ) oraz numer próbki. W odpowiedzi jest zwracana odpowiednia wartość sygnału wymuszającego. W module tym jest także zaimplementowana procedura definiująca zakłócenia.

konwers.pas - ze względu na brak dostatecznej ilości wolnego miejsca w obszarze zmiennych, dane z symulacji wymuszeniem skokowym są zapisywane bezpośrednio do pliku DANE.TMP. Aby mogły one być następnie przetworzone w innym programie, następuje konwersja do standardowego formatu przyjętego przez kolegów. Format tego pliku jest opisany w dalszej części dokumentacji.

sufler.pas, zasoby.pas - pliki zawierające dane do help'a oraz paska podpowiedzi (opis znajduje się dalej

Opis podstawowych procedur programu SIECI.EXE

Podstawowymi procedurami zawartymi w programie są procedury przeznaczone do symulacji działania pętli sterowania i implementacji sieci neuronowych. Poniżej zostaną omówione najważniejsze z nich:

Definicja zmiennych globalnych wykorzystywanych w procedurach.

	param_obie : array[0..7] of Real; {W tej tablicy przechowywane są parametry opisujące badany obiekt. Tablica ma rozmiar 8 liczb rzeczywistych ponieważ przyjęto, że maksymalnym wprowadzonym obiektem może być obiekt 4-tego rzędu. Np. dla obiektu przyjętego standardowo po uruchomieniu programu tablica zawiera następujące dane ( mamy tutaj n=3 i m=3 ): param_obie[0]=0.1; { a1 } param_obie[1]=0.02; { a2 } n = 3 param_obie[2]=0.03; {a3} param_obie[3]=0.1; { b1 } param_obie[4]=0.2; { b2 } m =3 param_obie[5]=0.3; { b3 } } patrz równanie ARMA ( 1 )
	ewagi,cwagi: array[1..8] of Real; {W tablicach tych są przechowywane wartości wag sieci neuronowych. Notacja jest podobna do powyższej. Waga ewagi[n+1] przyjmuje podczas inicjalizacji wartość 1.0. Przyjmując, że badany model zawiera parametry jak wyżej, indeks tej wagi jest ewagi[4]. Wszystkie podane wagi pochodzą z chwili (k-1). Odpowiednikiem zmienne ewagi[1..n+m] na rys. 4 są zmienne w1(k-1)..wn+m(k-1). Odpowiednikiem zmiennej cwagi[1..n+m] na rys. 5 są zmienne c1(k-1)..cn+m(k-1) }
	sygnal_u,sygnal_y : array[0..4] of Real; { Zmienne te reprezentują odpowiednio sygnały wyjściowe z regulatora neuronowego i z wyjścia badanego obiektu. Indeks w tablicy [0] oznacza próbkę w chwili bieżącej (k), natomiast pozostałe indeksy odpowiednio: [1] próbkę w chwili (k-1), [2] oznacza próbkę (k-2) itd. do indeksu [4]. Czyli maksymalne opóźniona próbka w obwodzie będzie (k-4) - ta.}
	y_estymowane, error, sygnal_we : Real; { Zmienna y_estymowane reprezentuje błąd predykcji - jest to różnica między wartością wyestymowaną przez neuronowy estymator a wartością z wyjścia badanego obiektu. Zmienna error jest to uchyb regulacji - różnica pomiędzy wartością zadaną a wartością z wyjścia badanego obiektu. Natomiast zmienna sygnal_we jest to wartość zadana czyli na rysunku nr 3 jest to zmienna y'(k+1). }

Odpowiedź badanego obiektu ARMA

procedure Odp_obiektu;

var
ysum,usum :Real;

  begin
                ysum:=0;
                usum:=0;

for i:=1 to n do
ysum:=ysum+sygnal_y[i]*param_obie[i];

for i:=n+1 to n+m do
usum:=usum+sygnal_u[i-n]*param_obie[i];

sygnal_y[0]:=usum-ysum;
end;

{zmienne pomocnicze}

{Zakładając, że n=3 j.w. można tę pętlę rozpisać:

sygnal_y[1]param_obie[1], czyli y(k-1)a1
sygnal_y[2]param_obie[2], czyli y(k-2)a2
sygnal_y[3]param_obie[3], czyli y(k-3)a3

Zakładając, że m=3 można tę pętlę rozpisać:

sygnal_u[1]param_obie[4], czyli u(k-1)b1
sygnal_u[2]param_obie[5], czyli u(k-2)b2
sygnal_u[3]param_obie[6], czyli u(k-3)b3

}

{odpowiedź obiektu w chwili bieżącej (k) }

Sygnał sterujący z regulatora neuronowego

procedure Wy_kontrolera;

var
wy_kontr :Real;

begin
wy_kontr:=0;
wy_kontr:=sygnal_we*cwagi[1];

for i:=0 to n-1 do
wy_kontr:=wy_kontr+(1sygnal_y[i+1]cwagi[i+2]);

end;

for i:=1 to m-1 do
wy_kontr:=wy_kontr+(-1sygnal_u[i]cwagi [i+n+1]);

{Zmienna pomocnicza }

{ y(k+1) * c1(k-1) na rys. 5}

sygnal_u[0]:=wy_kontr;
{ sygnał sterujący obiektem w chwili (k)

Implementacja estymatora neuronowego

procedure Wy_estymatora;

var
                ysum,usum :Real;
begin
               ysum:=0;
               usum:=0;

for i:=1 to n do
ysum:=ysum+sygnal_y[i]*ewagi[i];

for i:=n+1 to n+m do
usum:=usum+sygnal_u[i-n]ewagi[i];
y_estymowane:=usum-ysum;*

end;

{ zmienne pomocnicze }

{Na podstawie rysunku estymatora oraz założenia, że n,m=3 pętle te odpowiadają zapisowi:

y(k-1)w1(k-1),
y(k-2)w2(k-1),
y(k-3)*w3(k-1),

u(k-1)w4(k-1),
u(k-2)w5(k-1),
u(k-3)*w6(k-1)}

{ sygnał wyestymowany na podstawie wag i próbek z poprzednich chwil pobranych z wyjścia badanego obiektu }

Implementacja algorytmu Widrow-Hoffa modyfikującego wagi sieci

procedure Edelta;

var
                mianownik,licznik :Real;
                epsylon,alfa: Real;
                kod:Integer;

begin
mianownik:=0;
licznik:=0;

Val(DaneReguly.epsylon,epsylon,kod);
Val(DaneReguly.alfa,alfa,kod);

for i:=1 to n do
mianownik:=mianownik+sygnal_y[i]sygnal_y[i];
for i:=n+1 to n+m do
mianownik:=mianownik+sygnal_u[i-n] sygnal_u[i-n];
mianownik:=mianownik+epsylon;

licznik:=alfaerror;*

for i:=1 to n do
ewagi[i]:=ewagi[i]+(-1sygnal_y[i] licznik/mianownik);

{ zmienne lokalne pomocnicze }

{Zamiana wprowadzonych przez użytkownika parametrów definiujących uczenie sieci ( alfa i epsylon ) na wartości numeryczne ( użytkownik w Turbo Vision wprowadza je jako zmienne typu string ) }

{Obliczenie iloczynu macierzy : }

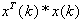{Zmienna error jest błędem predykcji

e(k)=y(k) - 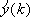, na rys. 4 : e(k-1)}

{ Tutaj następuje właściwa modyfikacja wektora wag neuronowego estymatora}

for i:=n+1 to n+m do

ewagi[i]:=ewagi[i]+(sygnal_u[i-n]licznik/mianownik);*

end;

W poniższej procedurze zostało zaimplementowane równanie (8) - modyfikacja wag neuronowego regulatora.

procedure Cdelta;

begin
cwagi[1]:=1.0/ewagi[n+1];

for i:=2 to n+1 do
cwagi[i]:=ewagi[i-1]/ewagi[n+1];

for i:=n+2 to m+n do
cwagi[i]:=ewagi[i]/ewagi[n+1];

end;

{ cwagi[1] według algorytmu są zawsze równe odwrotności zmiennej /ewagi[n+1]}

{Modyfikacja wag regulatora neuronowego polega zawsze na podzieleniu wag regulatora przez zmienną ewagi[n+1]}

Procedury dodatkowe

Przed każdym kolejnym procesem symulacyjnym tablice obsługujące algorytm sterowania (sieci neuronowe) powinny zostać wyzerowane. Realizuje to poniższa procedura:

procedure Zeruj_tablice;

begin
for i:=1 to 8 do

       begin
                ewagi[i]:=0;
                cwagi[i]:=0;
        end;

            for i:=0 to 4 do
                sygnal_y[i]:=0;

for i:=0 to 4 do
sygnal_u[i]:=0;
end;

Po każdym jednym cyklu symulacyjnym trzeba przepisać odpowiednio próbki z chwili (k) na (k-1) itd. Realizuje to procedura :

procedure Uporzadkuj_probki;

begin

    for i:=n downto 1 do
                sygnal_y[i]:=sygnal_y[i-1];
    for i:=m downto 1 do
                sygnal_u[i]:=sygnal_u[i-1];
end;

{ procedura prezentacji sygnałów z symulacji *}

repeat
if l>kol_probka then {wejscie do petli nastapi wtedy, gdy nadejdzie nowa probka}

begin
if (wysw_wag=0) then

             begin {Wyświetlanie zdefiniowanych parametrów na ekranie}
                  if (par_wysw and 1 =1) then rysuj_linie(l,40,wym_pop,sygnal_we,LightBlue,skala);
                 if (par_wysw and 2 =2) then rysuj_linie(l,40,blad_pop,error,LightCyan,skala);
                if (par_wysw and 4 =4) then rysuj_linie(l,40,blad_reg,uchyb,LightMagenta,skala)
               if (par_wysw and 8=8) then rysuj_linie(l,40,sygn_u_pop,sygnal_u[0],Yellow,skala/10);
              if (par_wysw and 16=16) then rysuj_linie(l,40,odp_y_pop,sygnal_y[0],LightRed,skala);

            end
                else
            begin {Wyświetlanie wag estymatora neuronwego}

                     for i:=1 to n+m do
                              rysuj_linie(l,40,pop_wagi[i],ewagi[i],i+7,500);
                                rysuj_linie(l,40,wym_pop,sygnal_we,LightGray,skala);
                    for i:=1 to 8 do
                             pop_wagi[i]:=ewagi[i];
              end;

if (NrWymuszenia.wymuszenie=0) and (l>100) and (l<=500) then

                begin
                     if sygnal_y[0]>y_max then y_max:=sygnal_y[0];
                    sygnal_sterujacy^[l-100]:=sygnal_u[0];
                    sygnal_wyjsciowy^[l-100]:=sygnal_y[0];
                    sygnal_uch^[l-100]:=uchyb;
                   jakosc_regul:=jakosc_regul+(uchybuchyb);* {Obliczanie jakości regulacji}
                end;

                                                wym_pop         :=sygnal_we;
                                                odp_y_pop      :=sygnal_y[0];
                                                blad_pop         :=error;
                                                sygn_u_pop    :=sygnal_u[0];
                                                blad_reg                 :=uchyb;
                                                kol_probka      :=l;

end;

until l=600; {Koniec kiedy zostanie pobrane 600 próbek}