SCHEDULING DIVISIBLE TASKS IN REGULAR
TOROIDAL MESH ARCHITECTURES
Maciej Drozdowski
Institute of Computing Science, Poznań University of Technology, Poznań, Poland
Plan of the presentation
1. Introduction
2. 2-Dimensional toroidal mesh
3. 3-Dimensional toroidal mesh
4. Closed form solutions
5. Conclusions
1 INTRODUCTION
WHAT IS A DIVISIBLE JOB?
DIVISIBLE JOB ¾ is a task (a computation, a program) which can be divided into parts of arbitrary sizes. These parts can be processed independently of each other on different processors.
In other words:
·
granularity of parallelism ¾ is fine,·
there are no data dependencies (precedence constraints).EXAMPLES OF DIVISIBLE JOBS
- distributed searching for a record in a database
- searching for a pattern in a text/audio/graphical file
- processing big measurement data files
- molecular dynamics simulations
- some problems of linear algebra
- some methods of solving partial differential equations
- parallel metaheuristics
DESCRIPTION OF DATA DISTRIBUTION
AND COMPUTATION PROCESSES
-
Initially all the load V to be processed resides on one processing element (PE) called ORIGINATOR.- Originator intercepts some part a 0 of the data for local processing, and sends the rest V-a 0 to its neighbors for remote processing.
- Processor i intercepts part a i of the received data and sends the rest to its still idle neighbors.
- This process is repeated until all the processors are activated.
- After completion of the computation the results may be returned to the originator.
Since data distribution takes place over a (relatively) slow network communication delays constitute important part of the total processing time.
Our goal is to find distribution of the load (data) among the processors such that the whole data communication and computation time is minimal possible.
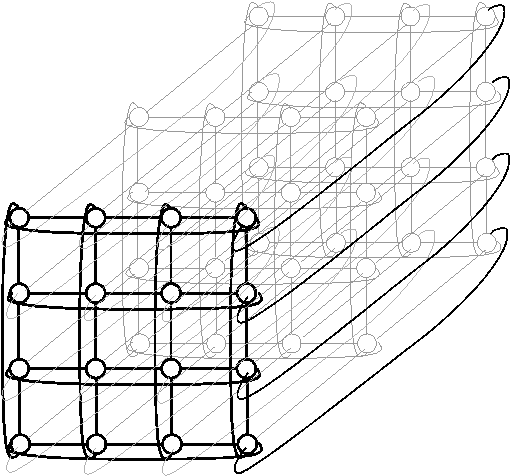
CONSIDERED ARCHITECTURE

Example 4´ 4´ 3 toroidal mesh
In toroidal mesh each PE can communicate simultaneously via:
p=1,…,4 ports in 2-dimensional toroidal mesh
p=1,…,6 ports in 3-dimensional toroidal mesh
p=1,…,2N ports in N-dimensional toroidal mesh
We assume that transmission time does not depend (significantly) on the distance (wormhole routing, circuit switching).
The transmission time of x units of data (e.g. bytes) is
tcomm
=S+Cxwhere:
S - communication stratup time [e.g. in seconds]
C - transfer rate [e.g. in seconds/byte]
Simultaneous computation and communication via each PE is possible.
The processing time for x units of data (e.g. bytes) is
tproc
=Ax
EARLIER RESULTS
- chain [BR92,CR88,GM94,...]
- star, bus [BR91,GM94,...]
- tree [CR90,BR92,BHR94,…]
- hypercube [BD95,BD97,D97]
- 2-D mesh, [BD96] (store and forward routing)
SUMMARY OF NOTIONS AND NOTATIONS
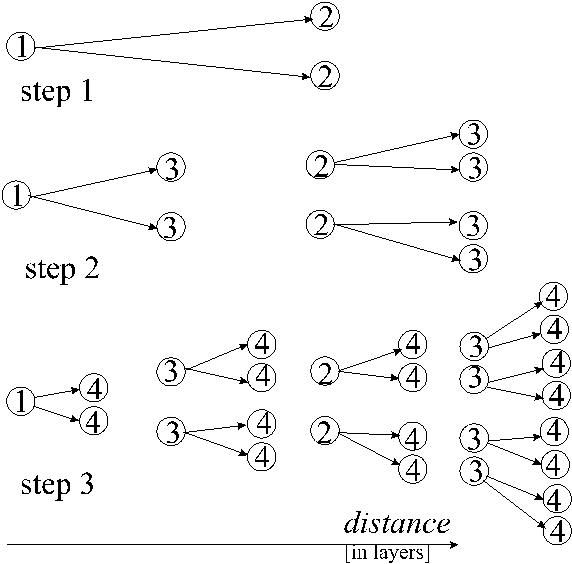
originator
- the PE that starts computationslayer - a set of processors activated in the same step of data scattering algorithm
V - the whole load to be processed (eg. in bytes)
a i - the load to be processed by PE i
p - the maximum number of ports that can be used by each PE
S - startup time [seconds]
C - transfer rate [seconds/byte]
A - processing rate [seconds/byte]
N - the number of layers
2 2-DIMENSIONAL TOROIDAL MESH
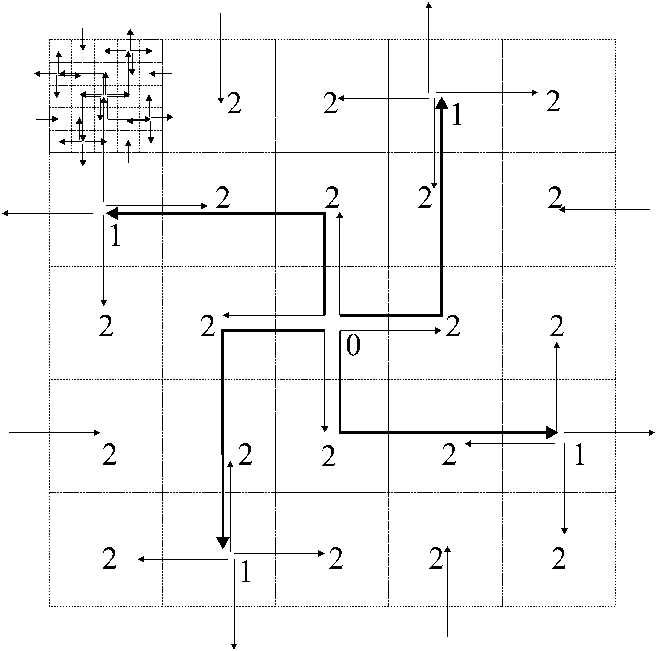
SCATTERING ALGORITHM
is a modification of Peters and Syska (1996) broadcasting algorithm.
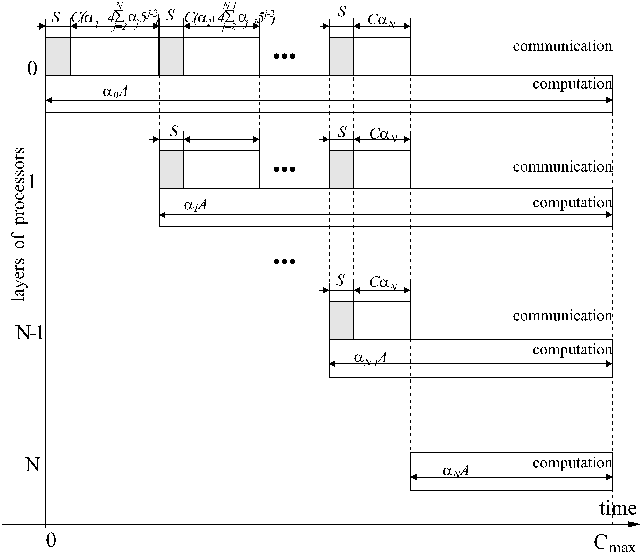
GANTT CHART
For simplicity of the presentation we assume that no results are returned.
Since nothing is returned, all PEs must stop processing at the same moment of time.
All processors in layer i receive the same amount a i of data.
Distribution of the load can be found from equations:
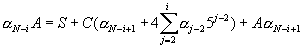 (i=1,...,N)
(i=1,...,N)
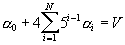
The above set of equations can be solved in O(N).
Execution time of the whole computation can be found as ![]() from this we can find speedup
from this we can find speedup 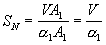 , and analyze performance of such a computer system.
, and analyze performance of such a computer system.
3. 3-DIMENSIONAL TOROIDAL MESH
Scattering methods for 3-Dimensional toroidal mesh depending on p – the number of ports used simultaneously
(examples for pÎ {1,2,3})
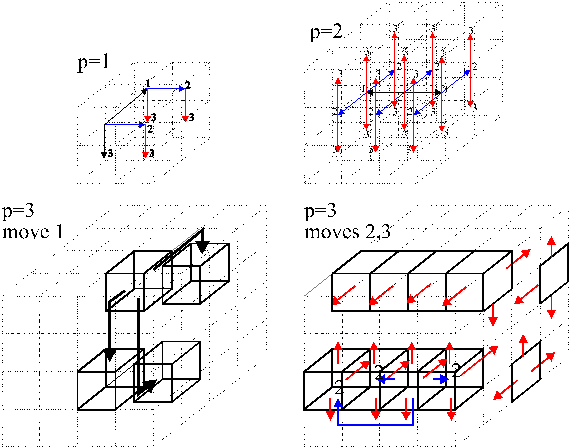
Diagram of data distribution for p=2
Note that the above methods
- use all p available ports simultaneously
- in 3 steps activate (p+1)3 times more PEs
- each processor receives data for itself and for its successors only once
- the Gantt chart is the same as for 2-D mesh, only p changes.
The distribution of the load can be found from the set of equations:
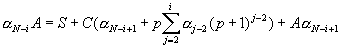 (i=1,...,N) (*)
(i=1,...,N) (*)
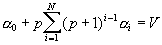
It can be solved for a i in time O(N).
4. CLOSED FORM SOLUTIONS
Solutions of equations (*) were found procedurally by solving numerically particular instances of the problem, for values of a i.
This method, though acceptable in practice, does not give an analytical solution (a formula).
The analytical solution would let draw conclusions on the analyzed architecture and scattering algorithm.
Such analytical solutions are called closed-form solutions.
Closed form solutions for (*) are as follows [DG97]
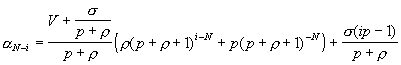 for i=1,...,N (**)
for i=1,...,N (**)
where: 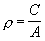
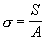
From (**) one can find
- Maximal number of usable layers:
a
N>0 Þ
![]() >0 Þ
>0 Þ
Þ
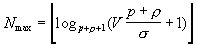
- Optimal number of layers from the point of view of speedup
![]() Þ
Þ
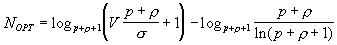
- Maximum possible speedup when N tends to infinity, when s <<V
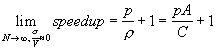
It can be shown that it is also an upper bound on the maximum speedup that can be obtained in any network with a single originator connected to the rest of the PEs over p ports.
5. CONCLUSIONS
We have presented methods of scheduling divisible job computations in toroidal mesh architecture.
Though the methods have some features of optimality:
- maximum number of ports p is always used,
- when ![]() then an upper bound on speedup is obtained,
then an upper bound on speedup is obtained,
it has not been proved that this method builds the shortest schedule.
Some other methods have potential of delivering shorter schedules in particular cases by e.g.:
- use of pipelining,
- sending to the layers with more processors first.
It even seems hard to devise a characteristic/feature on which a general optimality proof could be based.
Further research may include:
- nonlinear dependence of processing time on the volume of data
- many tasks sharing the mesh in space and time
- devising other (better?) scattering algorithms