Graf to po prostu zbiór wierzchołków połączonych ze sobą na różne sposoby
krawędziami. Skupię się tutaj na grafach skierowanych (rozróżnia się początkowy
i końcowy wierzchólek krawędzi). Nie będę rozważać multigrafów (czyli między
parą wierzchołków mogą wystąpić co najwyżej dwie krawędzie o przeciwnym
kierunku).
Liczbę wierzchołków będę oznaczać przez V (i numerować 1..V), a liczbę
krawędzi przez E. Oczywiście V2>=E. Grafy, w których
E=V2 nazywamy pełnymi, E jest trochę mniejsze od V2 -
gęstymi, a dużo mniejsze - rzadkimi.
Problem jest taki, że należy te grafy jakoś zapisać w pamięci.
Można go rozwiązać na kilka sposobów. Każdy ma swoje wady i zalety w zależności od
gęstości grafu i operacji na nim wykonywanych.
Chyba najprostszą reprezentacją, a zpewnością wymagającą najmniej wyobraźni,
jest lista krawędzi. To po prostu wrzucone na liste pary wierzchołków
(początki i końce krawędzi) bez żadnej specjalnej kolejności.
Ta metoda jest mało efektywna ze względu na to, że wykonanie dowolnej z powyższych operacji zmusza nas do przeszukania całej listy.
Macierz incydencji składa się z V wierszy (odpowiadającym wierzchołkom)
i E kolumn (odpowiadającym krawędziom). Na "skrzyżowaniu" wierzchołka
z krawędzią jest -1 gdy krawędź wychodzi z wierzchołka, +1 - krawędź wchodzi,
2 - pętla, 0 - brak incydencji.
Szczerze mówiąc jest to najgorsza z możliwych reprezentacji i nawet najgorszemu wrogowi nie życzyłbym wymyślenia takiej. Choć możliwe, że o czymś nie wiem, co uczyniłoby tą metodę choć trochę użyteczną.
Reprezentacja grafów przez listy sąsiedztwa, jak sama nazwa wskazuje, polega na trzymaniu dla każdego wierzchołka listy jego wszystkich sąsiadów (następników albo poprzedników).
Jest to moim zdaniem najlepsza reprezentacja: minimalna możliwa złożoność pamięciowa,
szybkie przeszukiwanie krawędzi wychodzących z danego wierzchołka, stosunkowo łatwa
implementacja.
Wadą jest jedynie długi czas sprawdzenia istnienia pojedyńczej krawędzi.
Można go poprawić do O(log V) wprowadzając drzewa BST (albo nawet drzewa
zrównoważone) zamiast list, ale to skomplikuje implementację. Jednak raczej
nie jest to potrzebne, bo wszystkie znane mi algorytmy nie korzystają z tej
operacji - opierają się jedynie na przejrzeniu listy następników wierzchołka.
Macierz sąsiedztwa ma wymiary VxV. Idea jest prosta: jeżeli na "skrzyżowaniu" i-tego wiersza i j-tej kolumny znajduje się 1 to znaczy, że istnieje krawędź (i,j) (wychodząca z i-tego wierzchołka i wchodząca do j-tego); jeśli 0 to znaczy, że tej krawędzi nie ma.
Wadą tej reprezentacji jest duża złożoność pamięciowa i czasy przejrzenia
większej liczby krawędzi. Dla grafów gęstych jest to niezauważalne, ale
dla grafów rzadkich zdecydowanie polecam poprzednią metodę.
Zaletą jest możliwość szybkiego sprawdzenia czy dana krawędź istnieje
(ale jak już wcześniej mówiłem, raczej to nie jest potrzebne).
Ale niepodwarzalną zaletą jest duża prostota implementacji - łatwo, szybko
i bezboleśnie.
Najbardziej skomplikowaną z powyższych reprezentacji jest macierz grafu,
wymyślona przez drużynę samego pdhiJB. Ma ona wymiary VxV, ale w odróżnieniu
od macierzy sąsiedztwa nie zawiera jedynie zer i jedynek, a liczby z trzech
możliwych przedziałów: (1) 1..V, (2) V+1..2*V, (3) -V..-1. Gdy liczba
w i-tym wierszu i j-tej kolumnie jest z przedziału (1) to istnieje krawędź (i,j);
gdy z przedziału (2) - istnieje krawędź (j,i); z przedziału (3) - nie istnieje
krawędź między i-tym i j-tym wierzchołkiem.
Cały jednak sekret polega na tym, że w tej liczbie zakodowany jest nie tylko typ
incydencji wierzchołków i-tego i j-tego, ale także "wskaźnik" na kolejny
wierzchołek będący z i-tym w takiej samej incydencji jak j-ty.
Tak na chłopski rozum to oto chodzi, że w i-tym wierszu macierzy są
schowane trzy listy: lista następników i-tego wierzchołka, lista jego poprzedników,
lista wierzchołków nieincydentnych z i-tym.
Mamy do czynienia z listami, więc trzeba zaznaczyć ich początki i końce.
Koniec można łatwo zaznaczyć w taki sposób, że ostatni element wskazuje na samego
siebie. Potrzebna nam jest dodatkowa struktura na zaznaczenie początków
wszystkich list (można użyć do tego osobnych tablic, albo dopisać je na skrajach
macierzy). Gdy jakaś lista jest pusta to można jako jej początek wpisać 0.
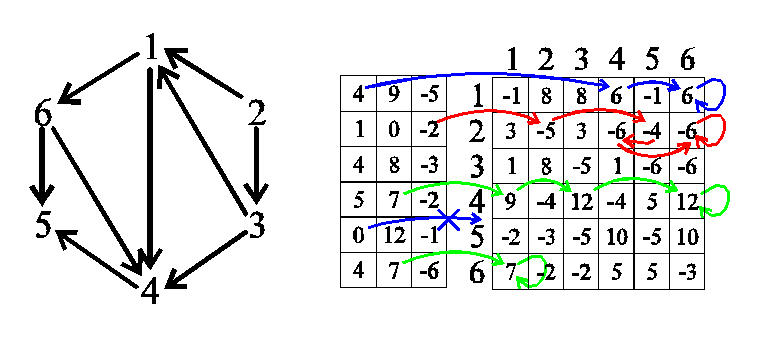
Wyjaśnienie jest nieco pokrętne, więc postanowiłem zaprezentować przykładowy
graf wraz z jedną z możliwych macierzy dla niego. Zaznaczyłem też strzałeczkami,
dla lepszego zrozumienia, kilka list (nie wszystkie, żeby nie zaciemniać rysunku),
zaszytych w wierszach macierzy. W trzech tablicach na lewo od macierzy
są zapisane początki odpowiednio list: następników, poprzedników,
braku incydencji.

Ta metoda jest ulepszeniem metody listowej o szybki czas sprawdzenia istnienia krawędzi, kosztem zwiększenia złożoności pamięciowej (która przy grafach gęstych wcale się nie pogarsza).