%matplotlib inline
from ipywidgets import *
import matplotlib.pyplot as plt
from IPython.display import set_matplotlib_formats
set_matplotlib_formats('svg')
import numpy as np
import scipy.stats as stats

def corr_plot(slope=1, sd=0, typ='kowariancja', show=False):
    x = np.linspace(0, 10, 100)
    y = slope * x + np.random.normal(0,sd,100)
    fig, axes = plt.subplots(figsize=(6,6))
    plt.scatter(x, y)
    c = np.corrcoef(x, y)[0][1] if typ=="korelacja" else np.cov(x,y)[0][1]
    c = round(c,3)
    title = "c="+str(c) if typ=='kowariancja' else "r="+str(c)
    if show:
        plt.title(title)
    plt.xlim(0,10)
    plt.ylim(-10,10)
    
def corr_examples(example="1", typ='kowariancja', show=False):
    x = np.linspace(1, 10, 100)
    y = -x**3 + np.random.normal(0,100,100) if example=="1" else np.cos(x) + np.random.normal(0,0.1,100)
    plt.scatter(x, y)
    if show:
        if typ=="korelacja":
            plt.title("r="+str(round(np.corrcoef(x, y)[0][1],3)))
        else:
            plt.title("c="+str(round(np.cov(x, y)[0][1],3)))

Korelacja i regresja liniowa

Kowariancja

• Kowariancja zmiennych losowych

$$\sigma^2_X = E[(X-\mu)^2]$$$$\sigma_{X,Y} = E[(X-\mu_x)(Y-\mu_y)]$$$$\sigma_{X,X} =?$$

• Estymator kowariancji

$$S_{XY}=\frac{1}{n-1}\sum_{i=1}^{n}(X_i-\bar{X})(Y_i-\bar{Y})$$

Przykład:

X	Y
1	5
2	6
3	1

mx = 2

my = 4

((1-2)(5-4)+(2-2)(6-4)+(3-2)(1-4))/2 = (-1+0-3)/2 = -2

interact(corr_plot, slope=(-1, 1, 0.1), sd=(0,10,1), typ=["kowariancja", "korelacja"])

<function __main__.corr_plot(slope=1, sd=0, typ='kowariancja', show=False)>

interact(corr_examples, typ=["kowariancja", "korelacja"], example=["1", "2"])

<function __main__.corr_examples(example='1', typ='kowariancja', show=False)>

• Kowariancja a niezależność zmiennych

$\;\;\;\;\;E[(X-\mu_x)(Y-\mu_y)] = E[XY - X\mu_Y-Y\mu_X+\mu_X\mu_Y]=E[XY]-E[X\mu_Y]-E[Y\mu_X]+\mu_X\mu_Y=E[XY]-\mu_X\mu_Y$

• Własności kowariancji
  • $\sigma_{X,Y} = \sigma_{Y,X}$
  • $\sigma_{X,k} = 0$
  • $\sigma_{kX,Y} = k\sigma_{X,Y}$
  • $\sigma_{X,Y+Z} = \sigma_{X,Y} + \sigma_{X,Z}$

Współczynnik korelacji liniowej Pearsona

• Korelacja zmiennych losowych

$$\rho=\frac{cov(X,Y)}{\sigma_X\sigma_Y}$$

• Estymator współczynnika korelacji

$$r = \frac{S_{XY}}{S_X S_Y} \frac{\sum_{i=1}^{n}(X_i-\bar{X})(Y_i-\bar{Y})}{\sqrt{(\sum_{i=1}^{n}(X_i-\bar{X})^2)(\sum_{i=1}^{n}(Y_i-\bar{Y})^2)}}$$

Przykład c.d.:

$S_X$ = 1

$S_Y$ = 2.646

$r = \frac{-2}{1*2.646} = -0.76$

interact(corr_plot, slope=(-1, 1, 0.1), sd=(0,10,1), typ=["kowariancja", "korelacja"])

<function __main__.corr_plot(slope=1, sd=0, typ='kowariancja', show=False)>

interact(corr_examples, typ=["kowariancja", "korelacja"], example=["1", "2"])

<function __main__.corr_examples(example='1', typ='kowariancja', show=False)>

Test na istotność współczynnika korelacji

• Układ hipotez:

$\;\;\;\;\;\;H_0: \rho=0$
$\;\;\;\;\;\;H_1: \rho > / \neq / < 0$

• Statystyka: $$t=\frac{r}{\sqrt{1-r^2}}\sqrt{n-2}~\sim~t(n-2)$$

Prosta regresja liniowa

interact(corr_plot, slope=(-1, 1, 0.1), sd=(0,10,1), typ=["kowariancja", "korelacja"])

<function __main__.corr_plot(slope=1, sd=0, typ='kowariancja', show=False)>

$Y = \hat{Y} + \epsilon$

$Y=\beta_0+\beta_1X+\epsilon$

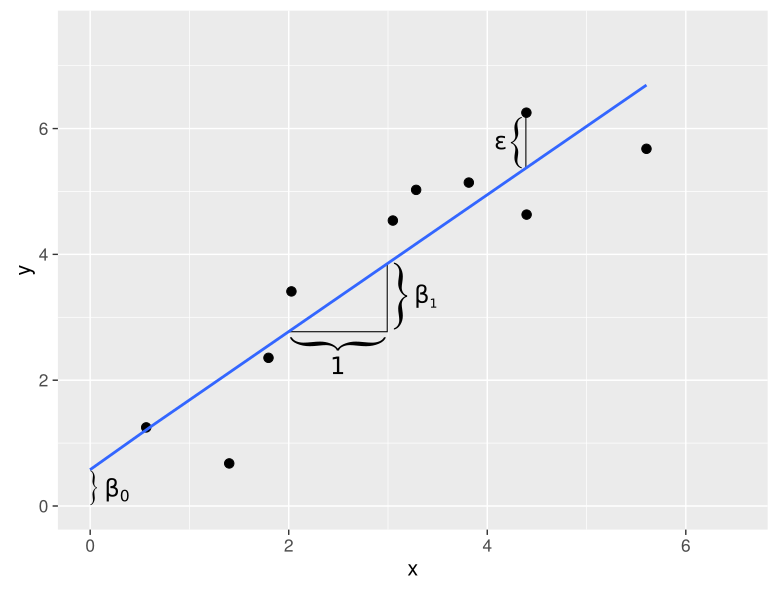
Założenia:

• Zależność liniowa między X i Y
• Wartości zmiennej niezależnej X są ustalone
• $\epsilon \sim N(0,\sigma^2)$

Metoda najmniejszych kwadratów

$Y=b_0+b_1X+e$

$\hat{Y}=b_0+b_1X$

$e_i=y_i-\hat{y_i}$

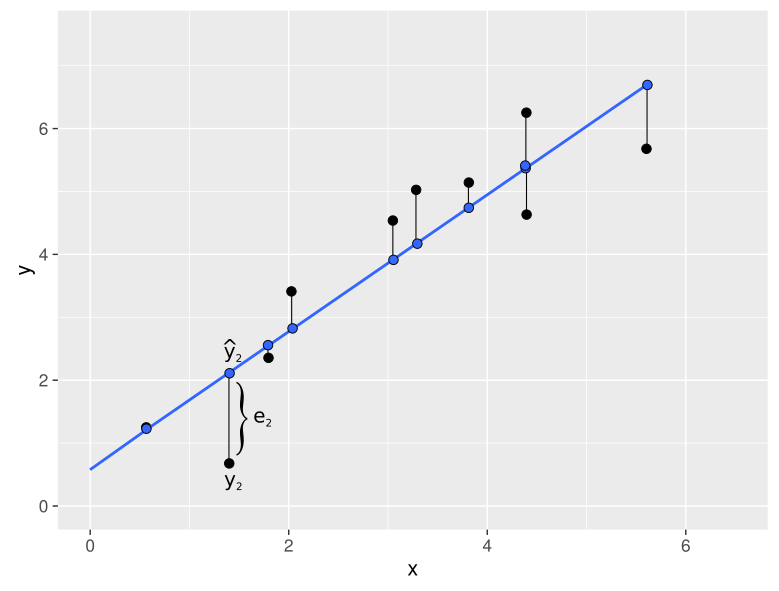
• Suma kwadratów rezyduów

$$S(b_0,b_1) = \sum\limits_{i=1}^n (y_i-\hat{y_i})^2 = \sum\limits_{i=1}^n(y_i-(b_1x_i+b_0))^2$$

• Wyraz wolny

$$b_0= \bar{y}-b_1\bar{x}$$

• Współczynnik kierunkowy

$$b_1 =\frac{s_{xy}}{s^2_x} = r\frac{S_Y}{S_X}$$

• prosta regresji przechodzi przez $(\bar{x}, \bar{y})$

• znak($b_1$) = znak($r$)

Przykład c.d. 2:

b1 = -2/1 = -2

b0 = 4 + 4 = 8

x = np.array([1,2,3])
y = np.array([5,6,1])
plt.scatter(x, y)
a = -2
b = 8
plt.plot(x, x*a+b)

[<matplotlib.lines.Line2D at 0x7fe9d788e5f8>]

Kwartet Anscombe’a

Źródło