%matplotlib inline
from ipywidgets import *
import matplotlib.pyplot as plt
from IPython.display import set_matplotlib_formats
set_matplotlib_formats('svg')
import numpy as np
import scipy.stats as stats

def regression(slope=5, sd=0, show=False):
    fig, axes = plt.subplots(figsize=(7,7))
    x = np.linspace(0, 1, 100)
    yt = 1 + slope * x
    plt.plot(x, yt)
    y = yt+ np.random.normal(0,sd,100)
    plt.scatter(x, y)
    my = np.mean(y)
    ssr = sum((yt-my)**2)
    sse = sum((y-yt)**2)
    sst = ssr+sse
    plt.ylim(-30,30)
    
    if show:
       plt.title("SST="+str(round(sst,2))+"   SSR="+str(round(ssr, 2))+"   SSE="+str(round(sse,2)))

Analiza regresji

interact(regression,slope=fixed(5), sd=(0,10,1))

<function __main__.regression(slope=5, sd=0, show=False)>

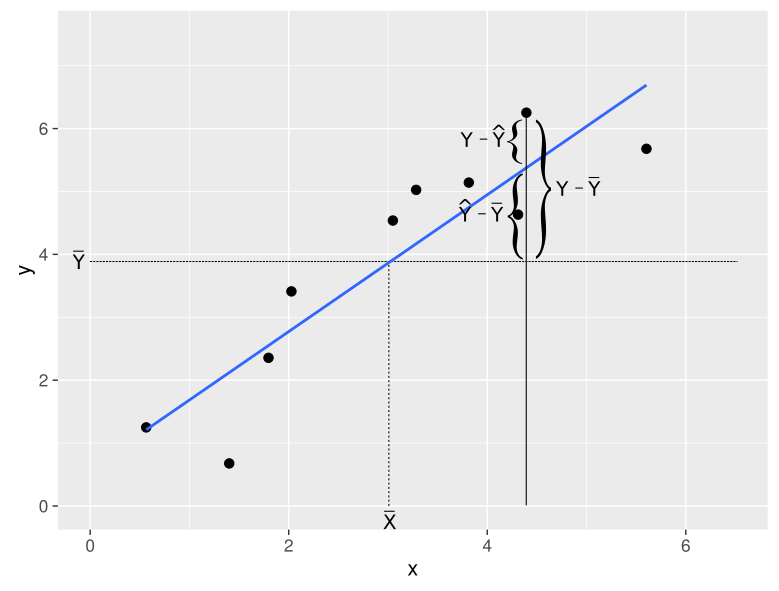
Rozkład zmienności Y

$$\underbrace{Y-\bar{Y}}_{\textrm{odchylenie całkowite}} = \underbrace{\hat{Y} - \bar{Y}}_{\substack{\textrm{odchylenie wyjaśnione} \\ \text{regresją}}} + \underbrace{Y-\hat{Y}}_{\substack{\text{odchylenie niewyjaśnione} \\ \text{regresją}}}$$

$$\underbrace{\sum\limits_{i=1}^n (y_i - \bar{y})^2}_{\substack{\text{całkowita suma} \\ \text{kwadratów odchyleń} \\ \text{SST}}} = \underbrace{\sum\limits_{i=1}^n (\hat{y_i}-\bar{y})^2}_{\substack{\text{regresyjna suma} \\ \text{kwadratów odchyleń}\\ \text{SSR}}}+\underbrace{\sum\limits_{i=1}^n (y_i-\hat{y_i})^2}_{\substack{\text{resztowa suma} \\ \text{kwadratów odchyleń}\\ \text{SSE}}}$$

interact(regression,slope=fixed(5), sd=(0,10,1))

<function __main__.regression(slope=5, sd=0, show=False)>

• dla $\hat{y}_i=y_i$:

  $$ SSE = \sum\limits_{i=1}^n (y_i-\hat{y_i})^2 = 0 $$

• dla $b_1=0$:

  $$SSR = \sum\limits_{i=1}^n (\hat{y_i}-\bar{y})^2 = \sum\limits_{i=1}^n (b_0+b_1x_i-\bar{y})^2=n(b_0-\bar{y})^2=n(\bar{y}-b_1\bar{x}-\bar{y})^2=0$$

Współczynnik determinacji

• Całkowita suma kwadratów odchyleń:

$$SST = SSR + SSE$$

• Współczynnik determinacji:

$$R^2 = \frac{SSR}{SST} = 1 - \frac{SSE}{SST}$$

• $R^2$ jest kwadratem współczynnika korelacji:

$$R^2 = \frac{SSR}{SST} = \frac{\sum\limits_{i=1}^n (\hat{y_i}-\bar{y})^2}{\sum\limits_{i=1}^n (y_i-\bar{y})^2} = \frac{\sum\limits_{i=1}^n (b_1x_i+b_0-\bar{y})^2}{\sum\limits_{i=1}^n (y_i-\bar{y})^2} = \frac{\sum\limits_{i=1}^n (b_1x_i+\bar{y}-b_1\bar{x}-\bar{y})^2}{\sum\limits_{i=1}^n (y_i-\bar{y})^2} = \frac{\sum\limits_{i=1}^n b_1^2(x_i-\bar{x})^2}{\sum\limits_{i=1}^n (y_i-\bar{y})^2} = b_1^2\frac{S_X^2}{S_Y^2}=r^2\frac{S_Y^2}{S_X^2}\frac{S_X^2}{S_Y^2}=r^2$$

• Skorygowany współczynnik determinacji:

$$R^2_{adj} = 1 - (1 - R^2) \frac{n-1}{n-k-1}$$

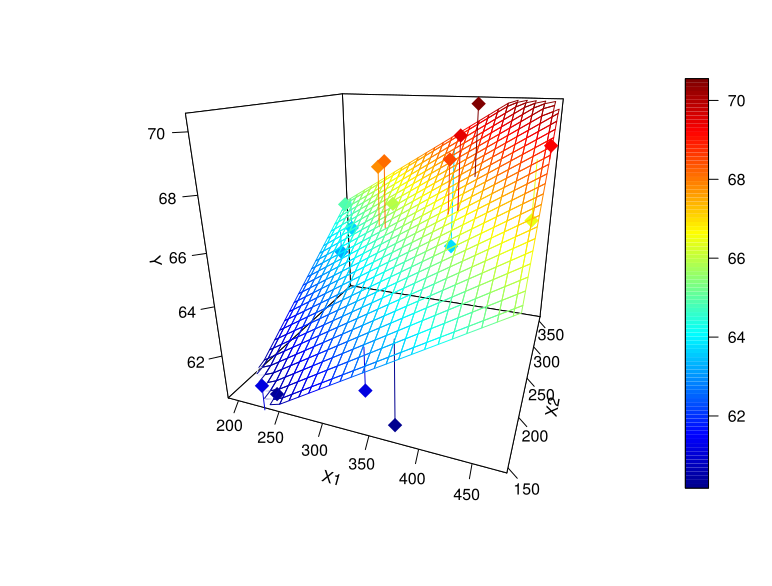
Regresja wieloraka

$Y=\beta_0+\beta_1X_1+\beta_2X_2+\epsilon$

Globalny test istotności (F)

• Układ hipotez:

$\;\;\;\;\;H_0: \beta_1=\beta_2=...=\beta_k=0$
$\;\;\;\;\;H_1:$ Nie wszystkie $\beta_i$ (i=1, 2, ..., k) sa równe $0$

• Statystyka testowa:
  • $n$ - liczba obserwacji
  • $k$ - liczba zmiennych objaśniających

Suma kwadratów odchyleń	df	Średnie odchylenie kwadratowe
SSR	k	$MSR=\frac{SSR}{k}$
SSE	n-(k+1)	$MSE = \frac{SSE}{n-(k+1)}$

$$F=\frac{MSR}{MSE} \sim F(k, n-(k+1))$$

Z próbki o liczności $n=24$ zbudowano model regresji wielorakiej wykorzystując 3 zmienne objaśniające. Uzyskano $SSR=36$ i $SSE=20$. Zweryfikuj statytyczną istotność modelu na poziomie $\alpha=0.05$.

$H_0: \beta_1=\beta_2=\beta_3=0$
$H_1:$ Nie wszystkie $\beta_i$ (i=1, 2, 3) sa równe $0$

$C_{kr}$ = (3.098, inf)

MSR=36/3=12

MSE= 20/(24-(3+1))=1

F=12/1=12

Odrzucamy $H_0$ na rzecz $H_1$

Test istotności parametru modelu (t)

• Układ hipotez:

$\;\;\;\;\;H_0: \beta_i=0$
$\;\;\;\;\;H_1: \beta_i\neq0$

• Statystyka testowa:

  $$t = \frac{b_i}{S(b_i)} \sim t(n-(k+1))$$

Standardowy błąd oszacowania

• Suma kwadratów błędów (rezyduów):

$$SSE = \sum(Y-\hat{Y})^2$$

• MSE:

$$MSE=\frac{SSE}{n-(k+1)}$$

• Standardowy błąd oszacowania:

$$S=\sqrt{MSE}$$

Błędy standardowe parametrów

$$S(b_0) = S * \sqrt{\frac{\sum\limits_{i=1}^nx_i^2}{n*\sum\limits_{i=1}^n(x_i-\bar{x})^2}}$$$$S(b_1) = S*\frac{1}{\sqrt{\sum\limits_{i=1}^n(x_i-\bar{x})}}$$

Wykresy diagnostyczne