In [1]:
%matplotlib inline
from ipywidgets import *
import matplotlib.pyplot as plt
from IPython.display import set_matplotlib_formats
set_matplotlib_formats('svg')
import numpy as np
import scipy.stats as stats
import matplotlib.patches as mpatches
In [2]:
def chi_sq(k=1):
    fig, axes = plt.subplots(figsize=(10,5))
    x = np.linspace(0, 80, 1000)
    chi2 = stats.chi2.pdf(x, k)
    plt.plot(x, chi2)
    plt.xlabel("x")
    plt.ylabel("f(x)")
    plt.title(r"$\chi^2($k="+str(k)+"$)$")
    plt.xlim(0,80)
    plt.grid()

def t_dist(k=1):
    fig, axes = plt.subplots(figsize=(10,5))
    x = np.linspace(-3.25, 3.25, 1000)
    t = stats.t.pdf(x, k)
    norm = stats.norm.pdf(x)
    plt.plot(x, t, label="t("+str(k)+")")
    plt.plot(x, norm, c='k', linestyle="--", label="N(0,1)")
    quant = -1.64
    plt.vlines(x=quant, ymin=0, ymax=stats.t.pdf(quant, k), color="#ff4c4c", alpha=0.5)
    x2 = np.linspace(-3.25, -1.64, 1000)
    t2 = stats.t.pdf(x2, k)
    plt.fill_between(x2, t2, color="#ff4c4c", alpha=0.5)
    plt.xlabel("x")
    plt.ylabel("f(x)")
    plt.title(r"$P(T<"+str(quant)+")="+str(round(stats.t.cdf(quant, k),3))+"$")
    plt.xlim(-3.25,3.25)
    plt.ylim(0, 0.42)
    plt.legend()
    plt.grid()
  
def norm_plain(mu, sigma):
    fig, axes = plt.subplots(figsize=(10,5))
    x = np.linspace(mu-3.25*sigma, mu+3.25*sigma, 1000)
    norm = stats.norm.pdf(x, mu, sigma)
    plt.plot(x, norm, mu, sigma)
    plt.xlabel("x")
    plt.ylabel("f(x)")
    plt.xlim(mu-3.25*sigma, mu+3.25*sigma)
    ymax = stats.norm.pdf(mu, mu, sigma)
    ymax += 0.025*ymax
    plt.ylim(0, ymax)
    plt.grid()
    
def norm(n=30, x_bar=98):
    mu = 100
    sigma = 15/np.sqrt(n)
    norm_plain(mu, sigma)
    quant = -1.64*sigma+mu
    plt.vlines(x=x_bar, ymin=0, ymax=stats.norm.pdf(x_bar, mu, sigma), color="k", alpha=0.5)
    x2 = np.linspace(mu-3.25*sigma, quant, 1000)
    norm2 = stats.norm.pdf(x2, mu, sigma)
    plt.fill_between(x2, norm2, color="#ff4c4c", alpha=0.5)
    plt.xlim(91, 109)
    
def conf_int(x_bar=98):
    n = 30
    mu = 100
    sigma = 15/np.sqrt(n)
    norm_plain(mu, sigma)
    alpha = 0.05
    quants = [stats.norm.ppf(a, mu, sigma) for a in [alpha/2, 1-alpha/2]]
    for start, end in zip([mu-3.25*sigma, quants[1]], [quants[0], mu+3.25*sigma]):
        x2 = np.linspace(start, end, 1000)
        norm2 = stats.norm.pdf(x2, mu, sigma)
        plt.fill_between(x2, norm2, color="#ff4c4c", alpha=0.5)
    quant = stats.norm.ppf(1-alpha/2)
    delta = quant*sigma
    lower, upper = x_bar-delta, x_bar+delta
    plt.scatter(x_bar, 0.001, c='r', zorder=2)
    plt.hlines(y=0.001, xmin=lower, xmax=upper, color='r')
    plt.vlines(x=lower, ymin=0, ymax=0.005, color='r')
    plt.vlines(x=upper, ymin=0, ymax=0.005, color='r')

Testy t i Z

Rozkład $\chi^2$

$Z_i \sim N(0,1)$

$$Q = \sum_{i=1}^{k}Z_i^2$$$$Q \sim \chi^2(k)$$
In [3]:
interact(chi_sq, k=(1,40,1))
Out[3]:
<function __main__.chi_sq(k=1)>

$E[Q]=k$

$D^2[Q] = 2k$

Rozkład t

$Z \sim N(0,1)$
$V \sim \chi^2(k)$

$$ T = \frac{Z}{\sqrt{\frac{V}{k}}} \sim t(k)$$
In [4]:
interact(t_dist, k=(1,100,1))
Out[4]:
<function __main__.t_dist(k=1)>

$E[T] = 0 \;\textrm{ dla }\; k > 1$

$D^2[T] = \frac{k}{k-2} \;\textrm{ dla }\; k > 2$

$\displaystyle \sum_{i=1}^{n}X_i^2 \sim \chi^2(n) \textrm{,}\;\; X_i \sim N(0,1)$

$\displaystyle \sum_{i=1}^{n}\left(\frac{X_i-\mu}{\sigma}\right)^2 \sim \chi^2(n) \textrm{,}\;\; X_i \sim N(\mu,\sigma)$

$\displaystyle \sum_{i=1}^{n}\left(\frac{X_i-\bar{X}}{\sigma}\right)^2 = \frac{(n-1)S^2}{\sigma^2} \sim \chi^2(n-1)$

$ T = \frac{\bar{X} - \mu}{S/\sqrt{n}} $ $= \frac{\frac{\bar{X} - \mu}{\sigma/\sqrt{n}}}{\sqrt{\frac{(n-1)S^2}{(n-1)\sigma^2}}}$ $= \frac{Z}{\sqrt{\frac{V}{(n-1)}}}\sim t(n-1) $

Test Z

  • $H_0: \mu = \mu_0$
    $H_1: \mu > / \neq / < \mu_0$
  • statystyka: $$\displaystyle Z=\frac{\bar{X}-\mu_0}{\frac{\sigma}{\sqrt{n}}}$$
  • zbiór krytyczny:
    • test prawostronny: $(z_{kr},\infty)$
    • test lewostronny: $(-\infty, -z_{kr})$
    • test dwustronny: $(-\infty, -z_{kr}) \cup (z_{kr},\infty)$

Test t

  • $H_0: \mu = \mu_0$
    $H_1: \mu > / \neq / < \mu_0$
  • statystyka: $$t=\frac{\bar{X}-\mu_0}{\frac{S}{\sqrt{n}}}$$
  • zbiór krytyczny:
    • test prawostronny: $(t_{kr},\infty)$
    • test lewostronny: $(-\infty, -t_{kr})$
    • test dwustronny: $(-\infty, -t_{kr}) \cup (t_{kr},\infty)$

Wybór testu

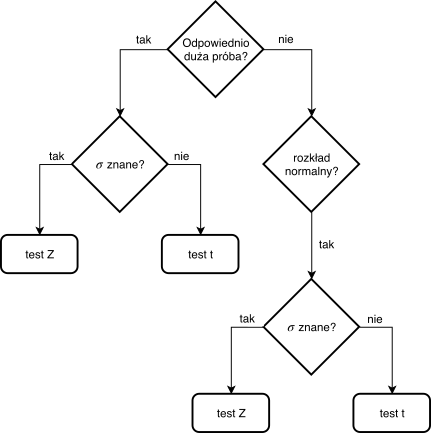
Wybór testu

Przykład

Zmierzono czas działania baterii 16 losowo wybranych smartfonów modelu X podczas przeciętnego użytkowania i otrzymano średni czas 22.5 godziny i odchylenie standardowe 4 godziny. Wiedząc, że czas działania baterii ma rozkład normalny sprawdź, czy dla modelu X jest on mniejszy niż 24 godziny.

$H_0: \mu = 24$
$H_1: \mu < 24$

$\alpha=0.05$

$C_{kr} = (-\infty, -t_{kr})$
$t(0.05, 15) = -1.75$
$C_{kr} = (-\infty, -1.75)$

$t=\frac{\bar{X}-\mu_0}{\frac{S}{\sqrt{n}}} = \frac{22.5-24}{\frac{4}{\sqrt{16}}}=\frac{-1.5}{1}=-1.5$

$t \not\in C_{kr}$

Brak podstaw do odrzucenia $H_0$

Test statystyczny a przedział ufności

In [5]:
interact(conf_int, x_bar=(90, 110, 1))
Out[5]:
<function __main__.conf_int(x_bar=98)>

Wpływ rozmiaru próby i istotność praktyczna

In [6]:
interact(norm, n=(30, 1000, 10), x_bar=(99, 100, 0.1))
Out[6]:
<function __main__.norm(n=30, x_bar=98)>