%matplotlib inline
from ipywidgets import *
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import scipy.stats as stats
from matplotlib.lines import Line2D
plt.rcParams["figure.figsize"] = (20,10)
plt.rcParams.update({'font.size': 22})

def describe(data):
    df = pd.DataFrame(data)
    print(df.describe())

def histogram(data, a=1, b=0):
    data = data*a+b
    plt.hist(x=data, bins='auto', color='#521422', alpha=0.7, rwidth=0.85)
    plt.grid(axis='y', alpha=0.75)
    plt.xlabel('X')
    plt.ylabel('Liczność')
    describe(data)
    plt.xlim(xmin=-13,xmax=13)
    
def normal_dist():
    x = np.linspace(-3, 3, 100)
    plt.plot(x, stats.norm.pdf(x, 0, 1))
    plt.grid()
    
def skewness(a=0):
    data = (stats.skewnorm(a).rvs(1000)*10).astype(int)
    
    _, _, patches = plt.hist(x=data, bins='auto', color='#521422', alpha=0.7, rwidth=0.85)
    plt.grid(axis='y', alpha=0.75)
    plt.xlabel('X')
    plt.ylabel('Liczność')
    
    stat = [np.mean(data), np.median(data), stats.mode(data)[0][0]]
    cols = ['r', 'g', 'b']
    lines = [Line2D([0], [0], color=c, lw=4) for c in cols]
    
    for col, st in zip(cols, stat):
        for i, patch in enumerate(patches):
            if st < patch.get_x():
                patches[i-1].set_color(col)
                break
            if i == len(patches)-1:
                patches[i].set_color(col)
     
    plt.suptitle("Skośność="+str(round(stats.skew(data),3)))
    plt.legend(lines,[txt +'='+str(stat[i]) for i, txt in enumerate(['Średnia', 'Mediana', 'Dominanta'])]) 

Statystyka opisowa

Źródło

Przykład - wyniki maratonu

Źródło

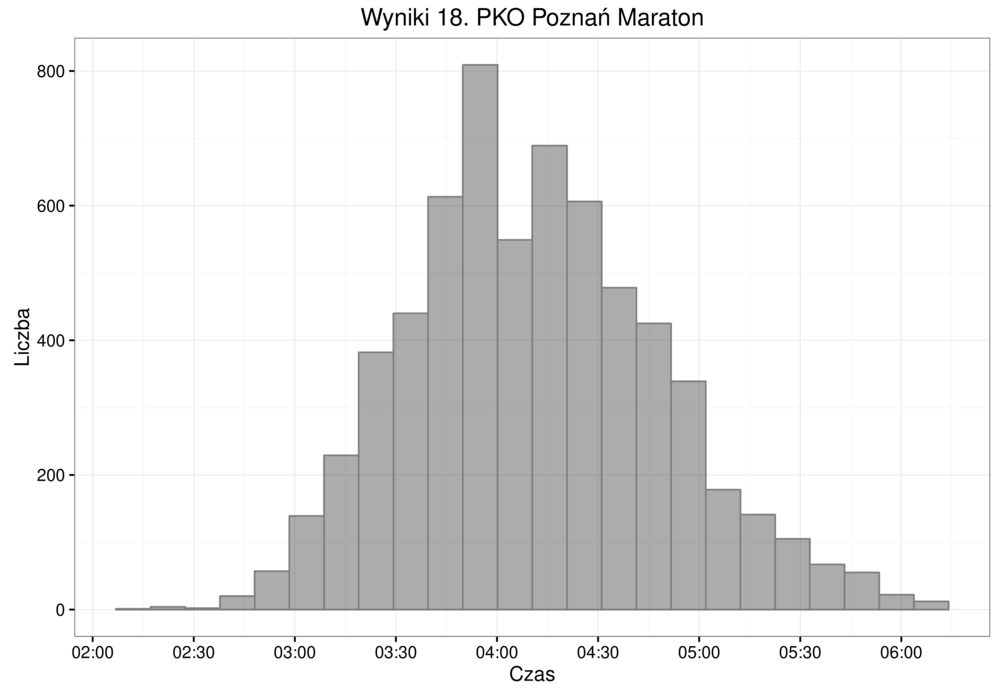
Przykład - wyniki maratonu 2

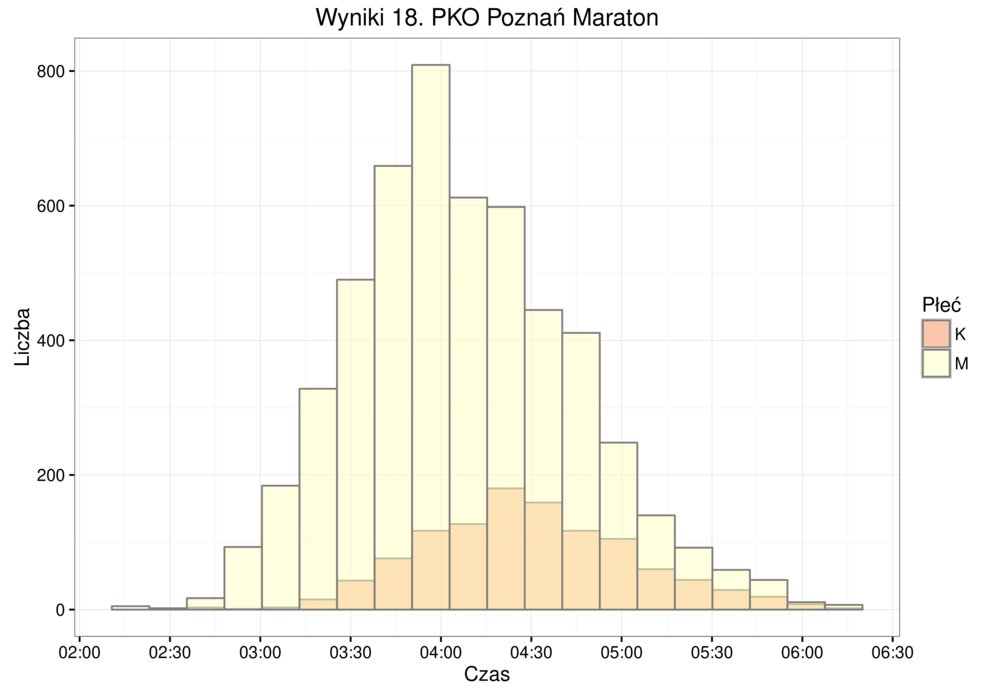
Miary rozkładu

\begin{itemize} \item Miary położenia \item Miary rozproszenia \item Miary asymetrii i koncentracji \end{itemize}

Dominanta

Dominantą nazywamy najczęściej występującą wartość w próbce.

Mediana

$n$ - liczba obserwacji \vspace{0.5cm}

\begin{itemize} \item $n$ nieparzyste $$\textrm{Mediana} = x_{(n+1)/2}$$ \vspace{0.25cm} \item $n$ parzyste $$\textrm{Mediana} = \frac{x_{n/2}+x_{n/2+1}}{2}$$ \end{itemize}

Inne kwantyle

\begin{itemize} \item Percentyle \item Decyle \item Kwartyle \item ... \end{itemize}$$Poz_p = (n+1)p$$

Źródło

Średnia arytmetyczna

\begin{itemize} \item w populacji: $$\mu = \frac{1}{n} \sum_{i=1}^{n}x_i$$ \item w próbce: $$\bar{x} = \frac{1}{n} \sum_{i=1}^{n}x_i$$ \end{itemize}

Źródło

Inne średnie

\begin{itemize} \item Średnia geometryczna $$\bar{x}_g = {\displaystyle \left(\prod _{i=1}^{n}x_{i}\right)^{\frac {1}{n}}={\sqrt[{n}]{x_{1}x_{2}\cdots x_{n}}}}$$ \item Średnia harmoniczna $$\bar{x}_h=\frac{n}{\sum\limits_{i=1}^{n}\frac{1}{x_i}} ~~~~~~~~~~~~~ \bar{x}_{wh}=\frac{\sum\limits_{i=1}^{n}w_i}{\sum\limits_{i=1}^{n}\frac{w_i}{x_i}}$$ \item Średnia ucinana $$\bar{x}_{t} = \frac{1}{n-2k}\sum_{i=k+1}^{n-k}x_i$$ \end{itemize}

Przykład - wynagrodzenia

Źródło

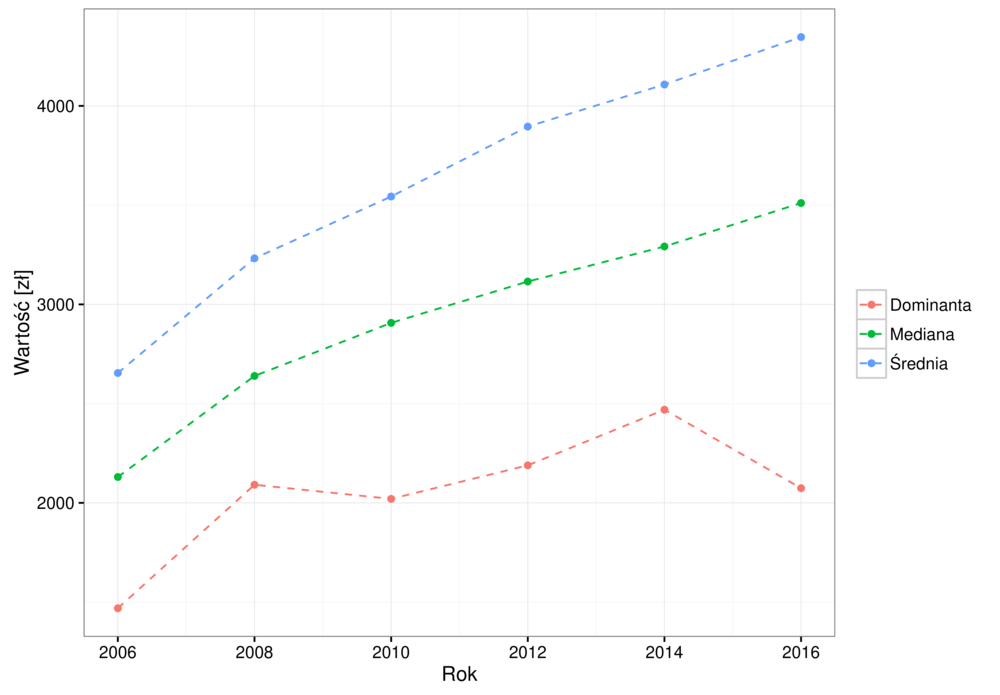
Skale pomiarowe

	Dominanta	Mediana	Średnia
Nominalne
Porządkowe
Interwałowe/Ilorazowe

Miary rozproszenia

\begin{itemize} \item ? $$\frac{1}{n}\sum_{i=1}^{n}(x_i-\bar{x})$$ \item Odchylenie przeciętne $$D = \frac{1}{n}\sum_{i=1}^{n}|(x_i-\bar{x})|$$ \end{itemize}

Wariancja i odchylenie standardowe

\begin{itemize} \item Wariancja w populacji $$\sigma^2=\frac{1}{n}\sum_{i=1}^{n}(x_i-\bar{x})^2$$ \item Wariancja w próbce $$s^2=\frac{1}{\boldsymbol{n}-\boldsymbol{1}}\sum_{i=1}^{n}(x_i-\bar{x})^2$$ \item Odchylenie standardowe $$s=\sqrt{s^2}$$ \end{itemize}

Inne miary rozproszenia

\begin{itemize} \item Rozstęp $$R = x_{max}-x_{min}$$ \item Rozstęp międzykwartylowy $$IQR = Q_3-Q_1$$ \item Współczynnik zmienności $$V = \frac{s}{\bar{x}}$$ \end{itemize}

data = np.random.normal(loc=1, scale=1, size=1000)    
describe(data)

                 0
count  1000.000000
mean      1.015359
std       1.019532
min      -1.906605
25%       0.338170
50%       1.008196
75%       1.691308
max       4.227062

interact(histogram, data=fixed(data), a=(-3,3,1), b=(-10,10,1))

<function __main__.histogram(data, a=1, b=0)>

Wykres pudełkowy (boxplot)

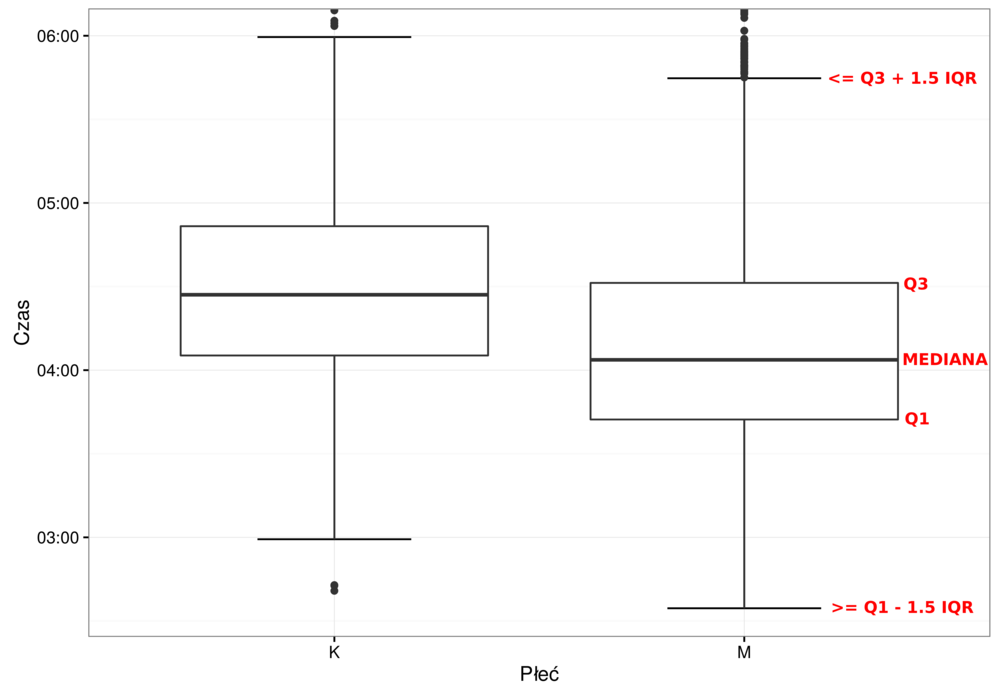
Miary asymetrii i koncentracji

Moment centralny rzędu \textit{k}

$$M_k = \frac{1}{n}\sum_{i=1}^{n}(x_i-\bar{x})^k$$

Współczynnik asymetrii (skośności)

$$A = \frac{M_3}{s^3}$$

Współczynnik wyostrzenia

\begin{itemize} \item Współczynnik koncentracji (kurtoza) $$K=\frac{M_4}{s^4}$$ \item Współczynnik wyostrzenia $$E=K-3$$ \end{itemize}

normal_dist()

interact(skewness, a=(-20,20,2))

<function __main__.skewness(a=0)>

Miary rozkładu dla szeregu rozdzielczego

Średnia i wariancja dla szeregu

$n_i$ - liczność $i$-tego przedziału

$\dot{x_i}$ - środek $i$-tego przedziału

\begin{itemize} \item Średnia: $$\bar{x_S} \approx \frac{\sum\limits_{i=1}^kn_i*\dot{x_i}}{n}$$ \item Wariancja: $$s^2_S \approx \frac{\sum\limits_{i=1}^kn_i*(\dot{x}-\bar{x})^2}{n-1}$$ \end{itemize}

Dominanta - szereg rozdzielczy

$$x_{modS} \approx x_0 + \frac{n_0 - n_{-1}}{(n_0 - n_{-1})+(n_0 - n_{+1})}*h_0$$

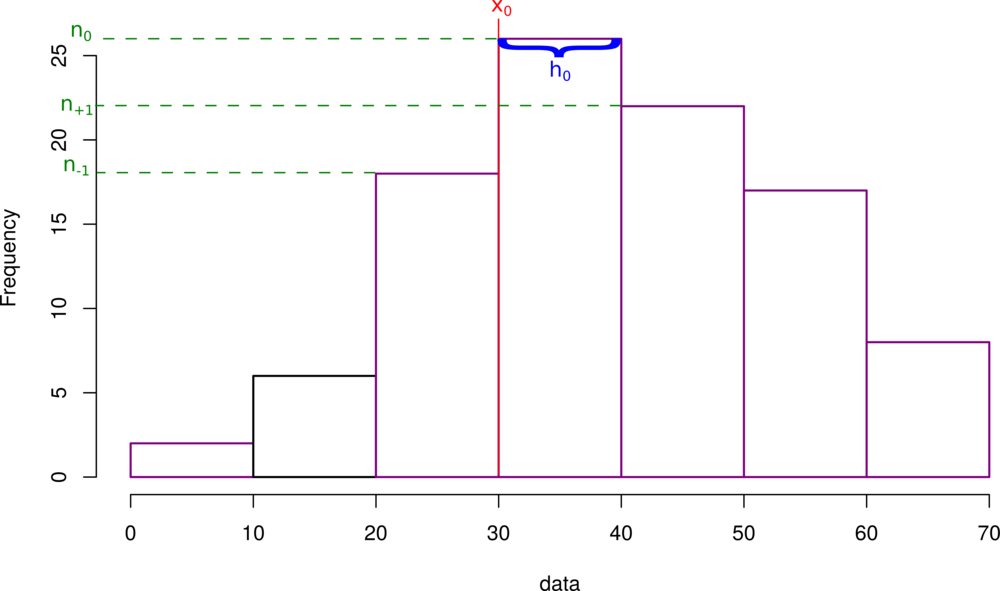
Mediana - szereg rozdzielczy

$$x_{medS} \approx x_0 + \frac{h_0}{n_0}*(\frac{n}{2}-F_{-1})$$

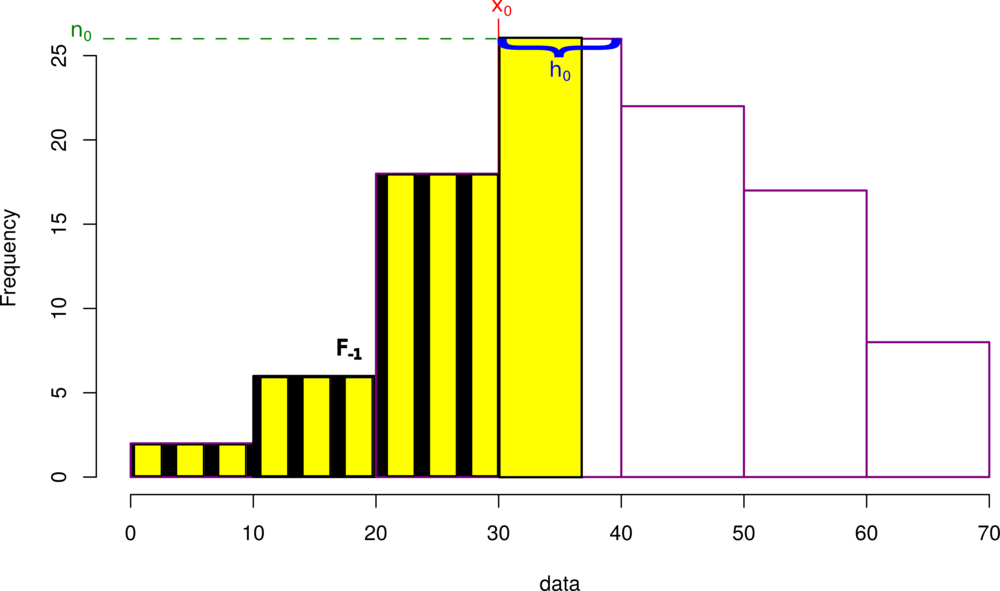
Skośność

$$A=\frac{\bar{x}-D}{s}$$